Question

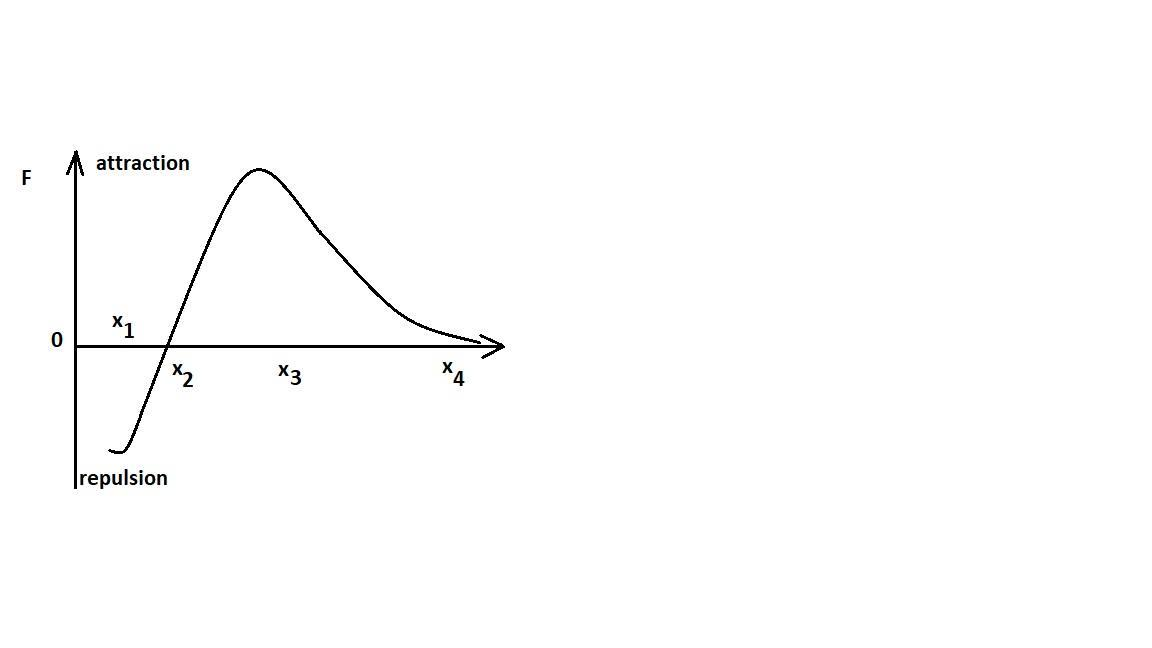
The diagram given shows how the net interaction force (conservative) between two particles $A$ and $B$ is related to the distance between them varies from \[{x_1}\] to \[{x_2}\] . Then
(A) Potential energy of the system increases from \[{x_1}\] to \[{x_2}\]
(B) Potential energy of the system increases from \[{x_2}\] to \[{x_3}\]
(C) Potential energy of the system increases from \[{x_3}\] to \[{x_4}\]
(D) KE increases from \[{x_1}\] to \[{x_2}\] and decreases from \[{x_2}\] to \[{x_3}\]

Answer 1

Hint: We will pull in the concept of potential energy to be the work done stored by the system. We will then try out the relationships and then finally find the correct option.
Formulae Used $F = - \frac{{dU}}{{dx}}$

Step By Step Solution
Firstly,
$F = - \frac{{dU}}{{dx}}$
Thus, we can say,
\[dU = - Fdx\]

Now,
Clearly,
When $F$ is positive, $dU$ is negative and when $F$ is negative, $dU$ is positive.
For the region from \[{x_1}\] to \[{x_2}\] , $F$ is negative as we can see from the graph itself.
Thus, $dU$ is positive.
Which means potential energy increases from \[{x_1}\] to \[{x_2}\].
Now,
Again for the region \[{x_2}\] to \[{x_3}\], $F$ is positive.
Thus, we can say $dU$ is negative.
Which means that potential energy decreases from \[{x_2}\] to \[{x_3}\].
Now,
For the region \[{x_3}\] to \[{x_4}\] , the force keeps on decreasing making it negative.
Thus,
$F$ is negative here.
Thus,
\[dU\] is positive.
Which means potential energy increases here.

Thus, taking all these observations into consideration, we can say (A) is the correct option.

Note: When $dU$ is positive, the potential energy increases because $dU$ refers to the change in the potential energy. When its value is positive, the final potential energy value is greater than the initial potential energy value. Thus making its overall value to be positive. The same analogy goes true when $dU$ is negative.