Question

The displacement of a particle as a function of time as shown in the figure. It indicates

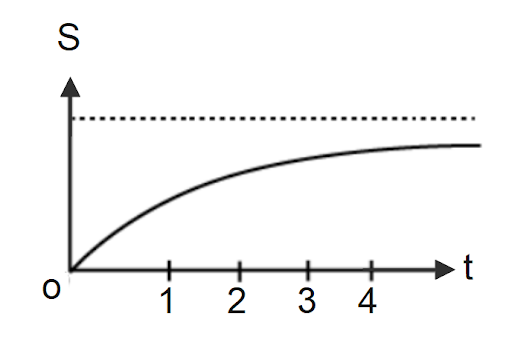
A. the particle starts with a certain velocity, but the motion is retarded and finally the particle stops.
B. the velocity of the particle decreases.
C. the acceleration of the particle is in the opposite direction to the velocity.
D. the particle starts with a constant velocity, the motion is accelerated and finally the particle moves with another constant velocity.

Answer 1

Hint: In this question, we are given a figure in which displacement of a particle is shown. We have to choose the option which our figure satisfies. We see that at origin slope is not zero and with the increase in time slope is decreasing. Then we choose the option which our figure satisfies.

Complete step by step solution:
We are given a figure in which the displacement of a particle as a function of time. We know that the slope of the s-t graph represents velocity. Initially at the origin, slope is not zero, so the particle has some initial velocity. With the increasing time we see that the slope is decreasing and finally the slope becomes zero, so the particle stops finally. As the magnitude of the velocity is decreasing, so the velocity and the acceleration will be in opposite directions.

Hence, options A,B and C are correct.

Note: We say that the displacement varies with time or is a function of time t.
We know the equation $d=vt+\dfrac{1}{2}a{{t}^{2}}$$d=vt+\dfrac{1}{2}a{{t}^{2}}$
This clearly shows that the displacement depends upon time.