Question

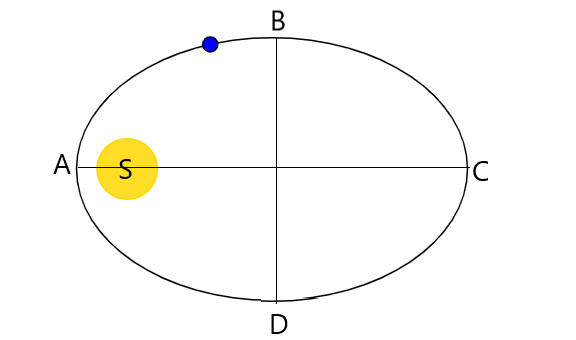
The earth E moves in an elliptical orbit with the sun S at one of the foci as shown in the figure. Its speed of motion will be maximum at the point
                           
(A) At A
(B) At B
(C) At C
(D) At D

Answer 1

Hint: We know that all the objects including the planets are attracted to each other by the force of gravity, this force is applied at the center so there is no change in angular momentum( L) i.e.L=constant.
Now we use the formula of angular momentum \[L = \vec p \times \vec r\] and find its magnitude i.e. \[L = p \times r \times \sin \theta \] and equate this equation with L=constant.
After equating we will find that velocity is inversely proportional to that of the particle in the orbit, so when radius is less, velocity will be more.

Complete step by step solution
As we know that all objects including planets are attracted to each other by a force of gravity. So, in our case we have earth and sun and earth is moving in an elliptical orbit with the sun S at one of the foci.
Earth and the sun are attracted to each other by a force of gravity and this force is applied to the center as gravitational force is a centered force.
We know that for any force applying on the center there is no change in angular momentum of the object, the angular momentum of the earth with respect to the sun is constant i.e. L=constant. This theory is based on the law of conservation of momentum.
The angular momentum of a particle of mass m w.r.t. a chosen origin is given by
 \[L = \vec p \times \vec r\] , where \[\vec p\] is the momentum of a particle and \[\vec r\] is the radius.
Now, the magnitude of the angular momentum is found from the definition of the cross-product, \[L = p \times r \times \sin \theta \], where \[\theta \] is the angle between \[\vec p\] and \[\vec r\] .
We know that angular momentum of a particle is given by \[\vec p = m \times \vec v\]
So, angular momentum of a particle of mass m is \[L = m \times v \times r \times \sin \theta \] , where m is the mass of the particle, v is the velocity of the particle.
Now, \[\theta = 90^\circ \] as with the definition of torque, we can define \[\vec r\] that is the perpendicular distance from the momentum vector \[\vec r\] to the origin.
Then, \[L = m \times v \times r\], as \[\sin 90 = 1\]
\[L = m \times v \times r\] =constant. The mass of any object is already constant, so \[v \times r\] =constant
We can say that \[v = \dfrac{1}{r}\]
According to this equation, where the planet distance is less velocity at that point is maximum.
As we can see in the figure, the nearest point of earth w.r.t sun is A. So, at point A the velocity will be maximum.

So, the correct option is A.

Note: In the case of planetary motion the angular momentum of the planet about the center of the sun remains constant. But in the case of linear momentum it does not remain constant.
Remember that for an orbit, angular momentum is conserved, and this leads to one of Kepler's laws that is ‘The Law of Areas’. This law discovered by Kepler arises from the conservation of angular momentum. When the earth is closer to the sun, it moves faster, sweeping through a longer path in a given time.
Also, the angular momentum of an isolated system remains constant in both magnitude and direction.