Question

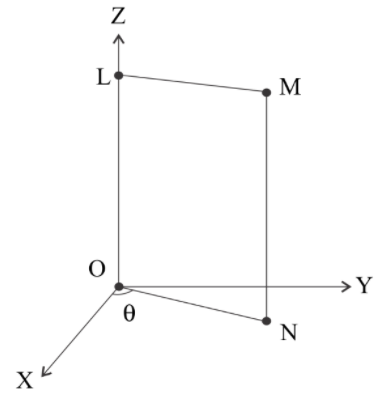
The electric field intensity at all points in space is given by $\vec E = \sqrt 3 \hat i - \hat j$ volts/ampere. A square frame LMNO of side 1 meter is shown in figure. The point N lies in the x-y plane. The initial angle between line ON and x-axis is $\theta = 60^\circ $. What is the magnitude of electric flux through the area enclosed in square frame LMNO?

A) 0 volt meter
B) 1 volt meter
C) 2 volt meter
D) 4 volt meter

Answer 1

Hint: The magnitude of the electric flux through the square frame is the dot product of the electric field intensity with the area of the frame.

Complete step by step solution:
The electric field intensity is given to us. The electric field intensity does not vary with position or time, thus it is a constant vector. The area of the square frame is 1 ${m^2}$. But the frame is at an angle of 60 degrees with the x-axis. So the area vector, denoted by $\vec S$, becomes,
$\vec S = 1\sin \left( {60^\circ } \right)\hat i + 1\cos \left( {60^\circ } \right)\left( { - \hat j} \right) = \dfrac{{\sqrt 3 }}{2}\hat i - \dfrac{1}{2}\hat j$
Now, we can find out the electric flux passing through the area enclosed by the square frame by taking the dot product of electric field intensity and area vector. On taking dot product, we obtain,
$\phi = \vec E \cdot \vec S$ …equation (1)
We now substitute the values of the vectors of area and electric field intensity in equation (1). We get,
$\phi = \left( {\sqrt 3 \hat i - \hat j} \right) \cdot \left( {\dfrac{{\sqrt 3 }}{2}\hat i - \dfrac{1}{2}\hat j} \right) = \dfrac{3}{2} + \dfrac{1}{2} = 2$ volt meter
Hence, the electric flux passing through the square frame is 2 volt meter.

Therefore, the correct answer of the question is option (C).

Note: The above question can also be solved by finding out the magnitude of the electric field intensity vector and area vector and then finding out the angle between these vectors to find out the electric flux passing through the square frame. But, doing that is more prone to errors because it will be relatively more calculation intensive.