Question

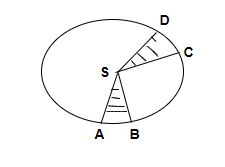
The figure represents an elliptical orbit of a planet around the sun. The planet takes time \[\mathop T\nolimits_1 \]​ to travel from A to B and it takes time \[\mathop T\nolimits_2 \]​ to travel from C to D. If the area CSD is double that of area ASB, then

(A) \[\mathop T\nolimits_1 = \mathop T\nolimits_2 \]
(B) \[\mathop T\nolimits_1 = \mathop {2T}\nolimits_2 \]
(C) \[\mathop T\nolimits_1 = \mathop {0.5T}\nolimits_2 \]
(D) Data insufficient

Answer 1

Hint: The given problem can be carried out by the consideration of the Kepler’s law of planetary motion. There are three laws of planetary motion given by the Kepler by the analysis of the whole astronomical data on the basis of Copernicus theory.

Complete step by step answer:
Step 1:

 The three laws of planetary motion given by the Kepler are as given below –
A) Kepler’s First law (Law of orbits): Every planet revolves around the sun in an elliptical orbit. The sun is situated at one foci of the ellipse.
B) Kepler’s Second law (Law of Areas): The line joining a planet to the sun sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant.
C)Kepler’s Third law (Law of periods): The square of the time period of revolution of a planet around the sun is directly proportional to the cube of semi major axis of its elliptical orbit,
i.e., \[\mathop T\nolimits^2 \propto \mathop R\nolimits^3 \]
Where, \[T = \] time taken by the planet to go once around the sun,
\[R = \] semi major axis of the elliptical orbit.

Step 2: This given can be solved using the Kepler’s second law i.e., the law of areas. As given in the problem, the planet takes time \[\mathop T\nolimits_1 \]​ to travel from A to B and it takes time \[\mathop T\nolimits_2 \]​ to travel from C to D.
So, according to second law, it can be seen that –
The area sweeps out by the planet in time \[\mathop T\nolimits_1 \] i.e., ASB is equal to the area sweeps out by the planet in time \[\mathop T\nolimits_2 \] i.e., CSD.
So, from the second law time will be equal so, \[\mathop T\nolimits_1 = \mathop T\nolimits_2 \] (1)
Now as per given condition if the area CSD is doubled that of area ASB i.e., area CSD = 2 (area ASB)
So, as per given by the law if the area is doubled then time taken by the planet to sweep out that area will be doubled.
\[\mathop T\nolimits_2 = 2\mathop T\nolimits_1 \]
On rearranging this equation, we will get –
\[\mathop T\nolimits_1 = \mathop {0.5T}\nolimits_2 \]
So, the option (C) is correct.

Note:
1) Kepler’s second law is based on the law of conservation of angular momentum.
2) The linear speed of the planet when the planet is closer to the sun is more than its linear speed when the planet is away from the sun.