Question

The graph between the time period and the length of the simple pendulum is a ____________.
A) straight line
B) curve
C) ellipse
D) parabola

Answer 1

Hint: The time period of a simple pendulum refers to the time taken to complete one oscillation by the bob. It depends only on the length of the pendulum and is found to be proportional to the square root of the length of the pendulum.

Formula Used:
The time period of a simple pendulum of length $L$ is given by, $T = 2\pi \sqrt {\dfrac{L}{g}} $ where $g$ is the acceleration due to gravity.

Complete step by step answer:
Step 1: Describe how the time period of the simple pendulum varies with its length.
A simple pendulum constitutes a bob attached to one end of an inextensible string of negligible mass and length $L$ with its other end fixed to a horizontal surface. The suspended bob is allowed to oscillate freely under the influence of gravity.
The time period of a simple pendulum is given by, $T = 2\pi \sqrt {\dfrac{L}{g}} $ ------- (1)
where $L$ is the length of the simple pendulum and $g$ is the acceleration due to gravity.
Equation (1) can also be expressed as, $T = \dfrac{{2\pi }}{{\sqrt g }}\sqrt L $
On squaring both sides we get, ${T^2} = \dfrac{{4\pi }}{g}L$ ------- (2)
Here, the acceleration due to gravity $g$ is constant. The only varying parameter is the length $L$ of the simple pendulum.
So, the equation (2) can be expressed as ${T^2} = kL$ where $k$ is a constant and $k = \dfrac{{4\pi }}{g}$
The equation ${T^2} = kL$ is similar to the equation of a parabola in the first quadrant given by, ${y^2} = 4a{x}$ where $a$ is a constant.
Therefore, the graph between the time period and length of a simple pendulum must be a parabola as shown below:

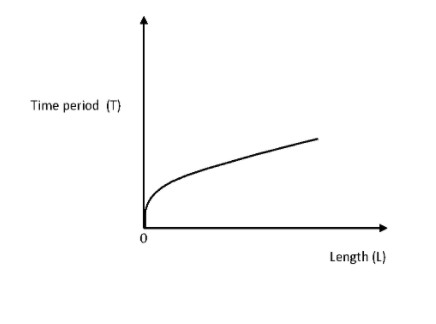
$\therefore$ The correct option is D.

Note: One oscillation of the simple pendulum corresponds to one complete to and fro motion of the bob. The bob, initially at rest, is raised to the left to induce oscillation. It will then move to the extreme position on the right side and then swing to the left to return to its starting point. This constitutes one oscillation. This is repeated. The time period of the pendulum is independent of the amplitude of oscillation. For a constant length, no matter how far the extreme positions of the bob are the period of oscillation remains the same.