Question

The graph shows the variation of displacement of a particle executing SHM with time. What do we infer from this graph?

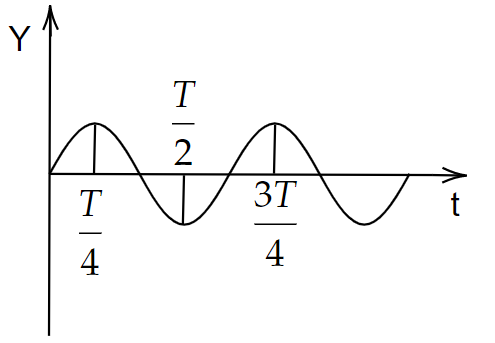
A. The force is zero at the time \[\dfrac{{3T}}{4}\]
B. The velocity is maximum at the time \[\dfrac{T}{2}\]
C. The acceleration is maximum at time T
D. The P.E is equal to total energy at the time \[\dfrac{T}{2}\]

Answer 1

Hint: Here, we need to recall the term SHM. A simple harmonic motion is a good example of periodic motion. In simple harmonic motion, a particle will be accelerated towards a fixed point and the acceleration of the particle is proportional to the magnitude of the displacement of the particle.

Complete step by step solution:

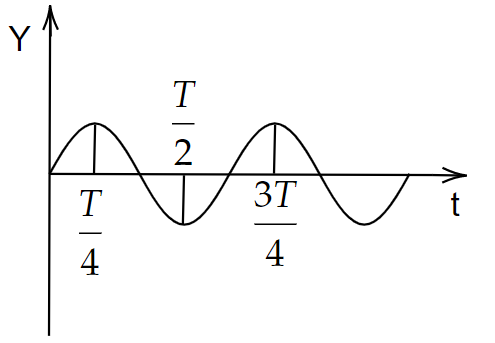
Image: Variation of displacement of a particle executing SHM with time.

The displacement versus time graph of a simple harmonic motion is represented as shown in the figure. Here the time periods are given as \[\dfrac{T}{4}\],\[\dfrac{T}{2}\],\[\dfrac{{3T}}{4}\] and T. If we consider the first option, at \[\dfrac{T}{4}\] the force acting on the particle is zero. If we see the position of the particle at the time interval \[\dfrac{T}{4}\] is nothing but extreme.

At an extreme position, we cannot say that force becomes zero. We know that at an extreme position the acceleration becomes maximum. Similarly, the second and third options are not correct.

If we consider the fourth option, at one point\[\dfrac{T}{2}\], the potential energy is in terms of total energy. This is correct because, at this particular point, the particle is in an extreme position, that is it is having a displacement -A with this displacement whatever the velocity means it becomes zero.

So once the velocity becomes zero, kinetic energy also becomes zero, then total energy must be exhibited in some other form, that is nothing but potential energy. Therefore, at time \[\dfrac{T}{2}\] the potential energy is in terms of total energy.

Hence, option D is the correct answer.

Note: Here, in this problem it is important to remember that, when the energy of a particle is converted into potential energy and kinetic energy or at which time period it will be converted and also about the simple harmonic motion.