Question

The moment of inertia of a rectangular lamina of mass 'm', length ' l ' and width ‘b' about an axis passing through its centre of mass, perpendicular to its diagonal and lies in the plane.
A) $\text{m}\left[ \dfrac{{{\ell }^{2}}+{{\text{b}}^{2}}}{12} \right]$
B) $\dfrac{\mathrm{m}}{12}\left[\dfrac{\ell^{4}+\mathrm{b}^{4}}{\ell^{2}+\mathrm{b}^{2}}\right]$
C) $\dfrac{\mathrm{m}}{6}\left[\dfrac{\ell^{4}+\mathrm{b}^{4}}{\ell^{2}+\mathrm{b}^{2}}\right]$
D) $\text{None of these}$

Answer 1

Hint: Moment of Inertia is the name given to rotational inertia, the rotational analog of mass for straight movement. It shows up in the connections for the dynamics of rotational movement. The moment of inertia must be determined regarding a picked pivot of revolution. For a point mass, the moment of inertia is only the mass multiplied by the square of perpendicular distance to the rotational axis, $I=m{{r}^{2}}$. That point mass relationship turns into the reason for all different moments of inertia since any item can be developed from an assortment of point masses.

Complete step by step answer:
To solve the given question, we must apply the concept of the moment of inertia.
We consider the given diagram to answer the given question,

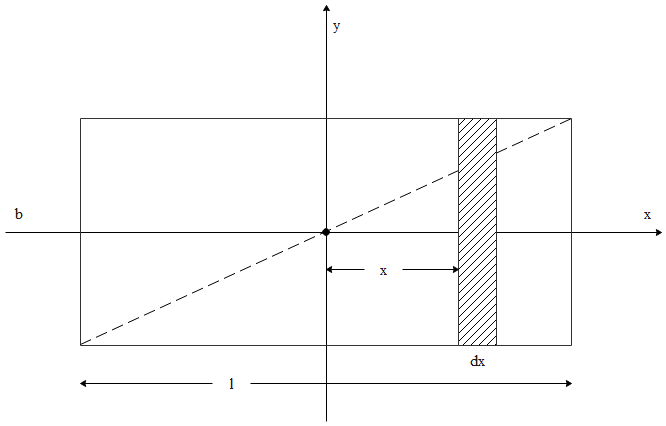
We can calculate the differential area as,
$\Rightarrow d A=b d x$
$\Rightarrow \sigma =\dfrac{M}{l\times b}$
Therefore,
$\Rightarrow dM=\sigma dA\Rightarrow \dfrac{Mdx}{lb}$
Integrating the values, we get,
$\Rightarrow \int{d}{{I}_{y}}=\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{d}M\times {{x}^{2}}$
$\Rightarrow {{I}_{y}}=\dfrac{M}{l}\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{{{x}^{2}}}dx$
$\Rightarrow \dfrac{M{{l}^{2}}}{12}$
Similarly, ${{I}_{y}}=\dfrac{M{{b}^{2}}}{12}$
$\Rightarrow {{I}_{z}}={{I}_{x}}+{{I}_{y}}=\dfrac{M{{b}^{2}}}{12}+\dfrac{M{{l}^{2}}}{12}$
$\Rightarrow M\left( \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \right)$

Therefore, the correct answer is Option A.

Note: Moment of Inertia is characterized as for a particular rotation axis. The moment of inertia of a point mass with deference toward a pivot is characterized as the result of the mass multiplied by the distance from the axis squared. The moment of inertia of any all-inclusive article is developed from that essential definition. The overall type existing apart from the moment of inertia includes an integral.