Question

The motion of a planet around the sun in an elliptical orbit is shown in the following figure. Sun is situated in one focus. The shaded areas are equal. If the planet takes time ${t_1}$ and ${t_2}$ in moving from $A$ to $B$ and from $C$ to $D$ respectively then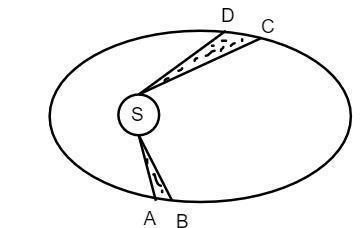
(A) ${t_1} > {t_2}$
(B) ${t_1} < {t_2}$
(C) ${t_1} = {t_2}$
(D) information incomplete

Answer 1

Hint: Kepler’s law is applicable for the motion of the planet which moves around the centre of gravity, sun. use this law to solve this problem. Rearranging the Kepler’s law and substituting both the areas are the same provides the relation between the time taken.
Useful formula:
The formula of the Kepler’s law of planetary motion is given by
$\dfrac{{dA}}{{dt}} = {\text{constant}}$
${t_1} = {t_2}$Where $dA$ is the change in the area and $dt$ is the change in the time taken to cover the area.

Complete step by step solution:
It is given that the Sun is the centre of the focus for the Earth to rotate in the elliptical path. From the given diagram and the given data, the shaded areas of $AB$ and $CD$ are the same. The time taken to cover the area of $AB$ is ${t_1}$ and the time taken to cover the area of $CD$ is ${t_2}$ .
Let us consider Kepler's law of the area of planetary motion. This law states that the line joining the sun and the planet will cover an equal area in the certain interval of time. This can also be said as the area velocity is constant.
$
  \dfrac{{dA}}{{dt}} = {\text{constant}} \\
  \dfrac{{{A_1}}}{{{t_1}}} = \dfrac{{{A_2}}}{{{t_2}}} \\
  {t_1} = \dfrac{{{A_1}}}{{{A_2}}}{t_2} \\
 $
Since the areas covered by both the lines are same, then ${A_1} = {A_2}$
${t_1} = {t_2}$
Hence the time taken will also be equal for both the areas.

Thus the option (C) is correct.

Note: Let us see the derivation of the Kepler’s law used in the above solution. It is known that the $L = \dfrac{{mA}}{t}$ , bringing $m$ to left hand side of the equation, we get, $\dfrac{L}{m} = \dfrac{A}{t}$ . Since the sun is the centre of gravity, the angular momentum is constant. The mass is also constant. So the $LHS$ is also constant. Hence $\dfrac{A}{t} = {\text{constant}}$ .