Question

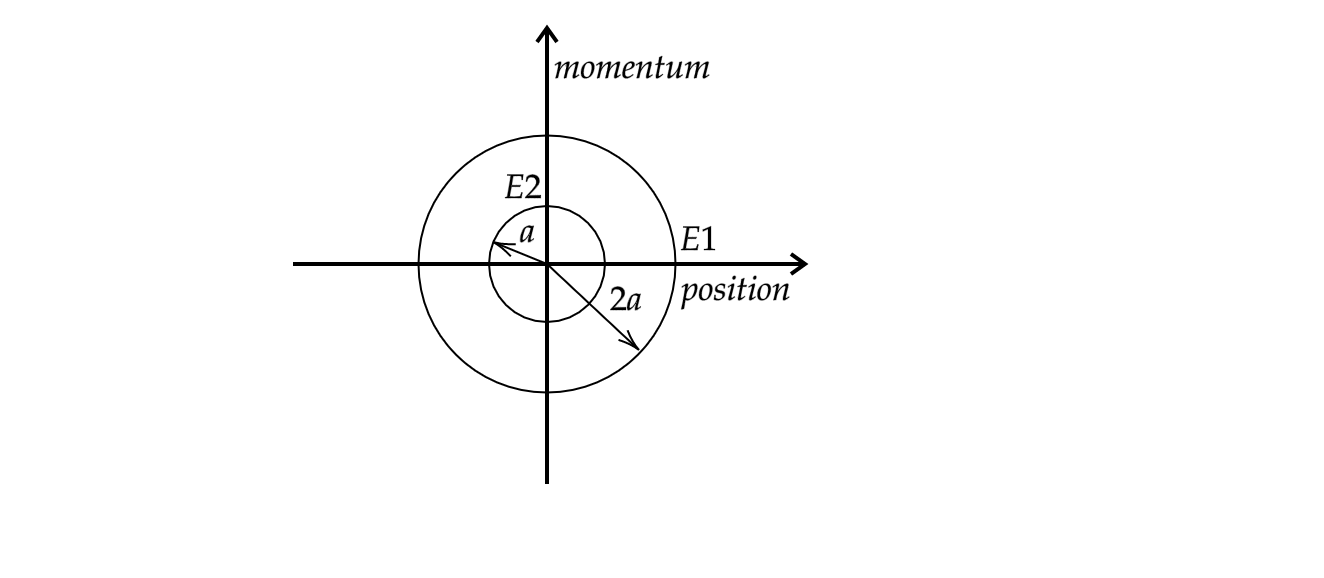
The phase space diagram for simple Momentum harmonic motion is a circle centred at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and \[{{E}_{1}}\] ,\[{{E}_{2}}\] are the total mechanical energies respectively. Then:

(A) \[{{E}_{1}}=\sqrt{2}{{E}_{2}}\]
(B) \[{{E}_{1}}=2{{E}_{2}}\]
(C) \[{{E}_{1}}=4{{E}_{2}}\]
(D) \[{{E}_{1}}=16{{E}_{2}}\]

Answer 1

Hint: The diagram given to us is the phasor diagram for the simple harmonic motion of the oscillator. The radius of the circle gives us the amplitude of oscillations of the oscillator and the angular velocity for the circle gives us the frequency of oscillation of the oscillator. We need to find the mechanical energy of the oscillator in the two cases.

Formula Used:
$\implies$ \[K=\dfrac{1}{2}m{{v}^{2}}\]
$\implies$ \[P=m\times v\]
$\implies$ \[K=\dfrac{{{P}^{2}}}{2m}\]

Complete step by step answer:
In case of simple harmonic motion, at the mean position of oscillation, the total mechanical energy appears in the form of kinetic energy and at the extreme positions, the total mechanical energy appears in the form of potential energy. Hence, the total mechanical energy of the oscillator is equal to the kinetic energy in the mean position.
The mean position of the oscillator is shown by the y-axis in the given figure. Since the momentum of the two cases is marked along the y-axis, we can say that \[{{P}_{1}}=2{{P}_{2}}\] where \[P\] denotes momentum of the oscillator.
From the equations \[K=\dfrac{1}{2}m{{v}^{2}}\] and \[P=m\times v\] , we can say that \[K=\dfrac{{{P}^{2}}}{2m}\] where \[P\] denotes momentum and \[K\] denotes kinetic energy of the particle in oscillation
Now, substituting the values of momentum for the two cases, we have
\[{{E}_{1}}=\dfrac{{{(2{{P}_{1}})}^{2}}}{2m}\] and \[{{E}_{2}}=\dfrac{{{P}_{1}}^{2}}{2m}\] where \[{{E}_{1}}\] and \[{{E}_{2}}\] are the total mechanical energies of the oscillations
Taking the ratio of the two energies obtained, we get
\[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{4}{1}\Rightarrow {{E}_{1}}=4{{E}_{2}}\]
Hence option (C) is the correct answer.

Note: We can alternatively solve this question with the help of the relation of kinetic energy in simple harmonic motion and the amplitude of the oscillation, that is \[K=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\] where \[K\] is the kinetic energy, \[\omega \] is the frequency of oscillation and \[A\] is the amplitude of oscillation. If we approach the question using this method, we won’t even need the diagram. We can just use the statement that their amplitudes are in the ratio \[2:1\] .