Question

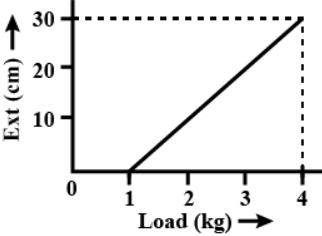
The pointer reading v/s load graph for a spring balance is as given in the figure. The spring constant is

(A) $0.1\,kg/cm$
(B) $5\,kg/cm$
(C) $0.3\,kg/cm$
(D) $1\,kg/cm$

Answer 1

Hint To find the answer, you first need to know that spring constant of a spring is nothing but the restoring force of a spring generated due to unit extension produced in the spring due to the external force applied on the spring. Mathematically,
$k = \dfrac{F}{x}$
You can use the graph to find the value of the spring constant very easily once you find the slope of the graph.

Complete step by step answer
As explained in the hint section of the solution to the question, we firstly need to know what spring constant is and how it is defined mathematically as relation of restoring force produced and the extension brought into the spring due to the force applied.
The spring constant, $k$ , is nothing but the representative of how stiff the spring is. Stiffer springs, i.e. springs which are more difficult to stretch by the application of same amount of force, have higher spring constants. The spring constant is thus the ratio of restoring force created in the spring due to a unit extension brought into the spring due to the application of some external force.
Mathematically, spring constant can be given as:
$k = \dfrac{{{F_r}}}{x}$
Where, $k$ is the spring constant of the spring,
${F_r}$ is the restoring force in the spring,
$x$ is the extension brought into the spring due to the application of some external force
If we observe the graph, we can see that the slop can be given as:
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Where, ${y_2},{y_1}$ are ordinates of the two points on the line in the graph and
${x_2},{x_1}$ are the abscissas of the two points on the line in the graph
If we find the value of the slope of the slope, we need to substitute the values of ordinates and abscissas of the two chosen points as:
$m = \dfrac{{20 - 10}}{{3 - 2}}\,cm/kg$
$ \Rightarrow m = 10\,cm/kg$
Also, since the y-axis is the extension in the spring while x-axis is the applied external force which is then gets nullified by the spring’s restoring force, the slope can also be taken as:
$m = \dfrac{x}{F}$
Where $x$ is the extension brought into the spring while,
$F$ is the external force applied.
Since the spring ultimately achieves equilibrium in each case, we can say that:
${F_r} = F$
Thus, we can write the spring constant as:
$k = \dfrac{1}{m}$
Substituting the value of the slope of the line in the graph, we get the value of spring constant as:
$
  k = \dfrac{1}{{10}}kg/cm \\
   \Rightarrow k = 0.1\,kg/cm \\
 $

As we can see, the correct answer to the question is option (A) since the value matches what we found out by solving the question.

Note Even though the value of force we took in the expression of spring constant and the slope turned out to be the same, remember that it would not be the same always. It was the same in our case as the spring was able to achieve equilibrium in each case and thus cancelled out the downwards force by the restoring force thus generated. Thus, the spring constant would not always be the same as the reciprocal of the slope of the graph.