Question

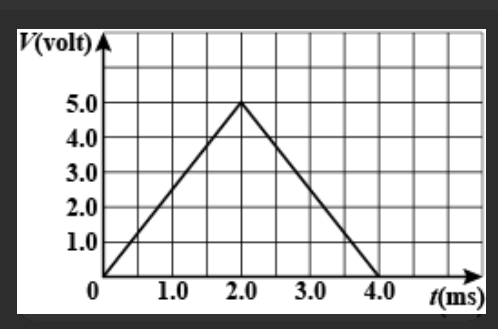
The potential difference across a $150 \mathrm{mH}$ inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when $t=4.0 \mathrm{ms} ?$


(A) $2.67 \times 10^{-4} \mathrm{A}$
(B) $3.67 \times 10^{-2} \mathrm{A}$
(C) $6.67 \times 10^{-2} \mathrm{A}$
(D) $9.67 \times 10^{-4} \mathrm{A}$

Answer 1

Hint: The electric potential difference between points A and B, VB−VA, is defined to be the change in potential energy of a charge q moved from A to B, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta. When a voltage is connected across a wire, an electric field is produced in the wire. Metal wire is a conductor. Some electrons around the metal atoms are free to move from atom to atom. This causes a difference in energy across the component, which is known as an electrical potential difference.

Complete step by step answer
If the electric potential difference between two locations is 1 volt, then one Coulomb of charge will gain 1 joule of potential energy when moved between those two locations. Because electric potential difference is expressed in units of volts, it is sometimes referred to as the voltage.
$\mathrm{V}_{\mathrm{L}}=\mathrm{L} \dfrac{\mathrm{d}}{\mathrm{dt}}$
$\therefore \quad \mathrm{di}=\dfrac{1}{\mathrm{L}}\left(\mathrm{V}_{\mathrm{L}} \mathrm{dt}\right)$
$\therefore \quad \int \mathrm{di}=\mathrm{i}=\dfrac{1}{\mathrm{L}} \int \mathrm{V}_{\mathrm{L}} \mathrm{dt} \quad$ or $\quad \mathrm{i}=\dfrac{1}{\mathrm{L}}$
At $\mathrm{t}=4 \mathrm{ms}$
$\mathrm{i}=\left(150 \times 10^{-3}\right)^{-1}\left(\dfrac{1}{2} \times 4 \times 10^{-3} \times 5\right)=6.67 \times 10^{-2} \mathrm{A}$

So the correct answer is option C.

Note: One volt is defined as the difference in electric potential between two points of a conducting wire when an electric current of one ampere dissipates one watt of power between those points. Voltage, also sometimes called potential difference or electromotive force (EMF), refers to the amount of potential energy the electrons have in an object or circuit. In some ways, you can think of this as the amount of "push" the electrons are making to try to get towards a positive charge. This process defines the electric potential of a point-like charge. Therefore, a system consisting of a negative and a positive point-like charge has a negative potential energy.