Question

The radius of a sector is 12 cm and the angle is \[120^\circ \]. By joining its straight sides a cone is formed. Find the volume of that cone.

Answer 1

Hint: First, we will find the value of the radius by using the formula of circumference of the circle, \[2\pi r\], where \[r\] is the radius of the circle and then the formula to calculate the volume of a cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base of cone and \[h\] is the height of a cone.

Complete step-by-step solution
It is given that the radius of a sector is 12 cm and the angle is \[120^\circ \].



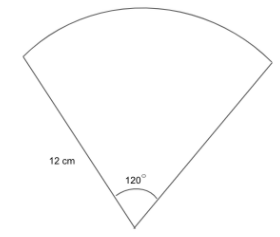
Let us assume that the radius of the given cone is \[r\].

If joining the straight side forms a cone then the height of a cone is equal to the radius of the sector.

Thus, we have \[h = 12{\text{ cm}}\].

Also the perimeter of the circular part of the cone is equal to the length of the area.

We know that the circumference of the circle or perimeter of the circle is the measurement of the boundary across any two dimensional circular shape including the circle.

We also know that the formula to calculate the circumference of the circle is \[2\pi r\], where \[r\] is the radius of the circle.

From the above formula of the circumference of the circle and the values of height and angle, we get

\[
   \Rightarrow 2\pi r = 2\pi \times 12 \times \dfrac{{120}}{{360}} \\
   \Rightarrow 2\pi r = 2\pi \times 4 \\
   \Rightarrow 2\pi r = 8\pi \\
 \]

Dividing the above equation by \[\pi \] on each of the sides, we get

\[
   \Rightarrow \dfrac{{2\pi r}}{\pi } = \dfrac{{8\pi }}{\pi } \\
   \Rightarrow 2r = 8 \\
 \]

Dividing the above equation by 2 on each of the sides, we get

\[
   \Rightarrow \dfrac{{2r}}{2} = \dfrac{8}{2} \\
   \Rightarrow r = 8 \\
 \]

Thus, the radius of the given cone is 8 cm.

We will use the formula to calculate the volume of a cone is \[\dfrac{1}{3}\pi {r^2}h\], where \[r\] is the radius of the base of cone and \[h\] is the height of a cone.

Substituting the values of \[h\] and \[r\] in the above formula, we get

\[
  {\text{Volume of cone}} = \dfrac{1}{3} \times 3.14 \times 16 \times 12 \\
   = 3.14 \times 16 \times 4 \\
   = 200.96{\text{ c}}{{\text{m}}^3} \\
 \]

Thus, the volume of a cone is \[200.96{\text{ c}}{{\text{m}}^3}\].

Note: In solving these types of questions, you should be familiar with the formula of calculating the volume of a cone. Some students use the formula of area of a cone instead of the volume of a cone, which is wrong. In this question, we have to carefully analyze the transformation of converting the sector into the cone. After that, we will use the required conditions and then the problem is simple. Also, always remember to write the units, else your answer will be incomplete.