
The relation between $\theta $, b and D is:
(where $\theta $ is the parallax angle, b is the distance between two points of separation, D is the distance of source from any point of observation)
A. $\theta = \dfrac{b}{D}$
B. $\theta = \dfrac{D}{b}$
C. $\theta = b \times D$
D. $\theta = {b^2} \times D$
Answer
232.8k+ views
Hint To answer this question at first we should have been very much clear with the figure. From the figure we have to find the value of tan $\theta $. The expression for tan $\theta $ will give us the required answer to this question.
Complete step by step answer
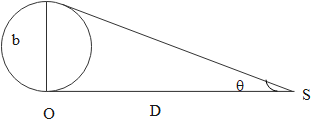
Since we have to consult the figure for finding the relationship between $\theta $, b and D, let us first be familiar with this. So given below is the diagram:
As we know that we have to find the value for tan $\theta $, from the figure it is clear that:
$\tan \theta = \dfrac{b}{D}$.
Here as mentioned $\theta $ is the parallax angle, b is the distance between two points of separation, D is the distance of source from any point of observation.
We know that $\theta $ is a very small angle. So the value of tan $\theta $ will be very less as well. Therefore there will not be much difference between tan$\theta $ and $\theta $. So for our convenience we can assume that:
$\tan \theta \sim \theta $
So we get from the figure that:
$\theta = \dfrac{b}{D}$
So we can say that the relation between $\theta $, b and D is $\theta = \dfrac{b}{D}$.
Hence the correct answer is option A.
Note In the answer we have come across the term parallax angle. For better understanding we have to understand the meaning of this term. By parallax angle we mean the angle that is formed between the Earth at a specific time of the year and again the Earth, but this time it is only 6 months later.
From the parallax formula we get this idea that the distance of a star will be equal to 1 divided by that of the parallax angle. The parallax angle is measured in arc-seconds and the distance is measured in parsecs.
Complete step by step answer
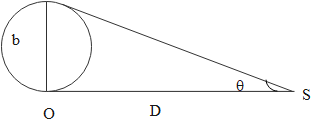
Since we have to consult the figure for finding the relationship between $\theta $, b and D, let us first be familiar with this. So given below is the diagram:

As we know that we have to find the value for tan $\theta $, from the figure it is clear that:
$\tan \theta = \dfrac{b}{D}$.
Here as mentioned $\theta $ is the parallax angle, b is the distance between two points of separation, D is the distance of source from any point of observation.
We know that $\theta $ is a very small angle. So the value of tan $\theta $ will be very less as well. Therefore there will not be much difference between tan$\theta $ and $\theta $. So for our convenience we can assume that:
$\tan \theta \sim \theta $
So we get from the figure that:
$\theta = \dfrac{b}{D}$
So we can say that the relation between $\theta $, b and D is $\theta = \dfrac{b}{D}$.
Hence the correct answer is option A.
Note In the answer we have come across the term parallax angle. For better understanding we have to understand the meaning of this term. By parallax angle we mean the angle that is formed between the Earth at a specific time of the year and again the Earth, but this time it is only 6 months later.
From the parallax formula we get this idea that the distance of a star will be equal to 1 divided by that of the parallax angle. The parallax angle is measured in arc-seconds and the distance is measured in parsecs.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




