Question

The tangent at $P$ to a parabola \[{{y}^{2}}=4ax\] meets the directrix at \[U\] and the base of the latus rectum at \[V\], then $SUV$ (where $S$ is the focus) must be a/an
(a). right triangle
(b). equilateral triangle
(c). isosceles triangle
(d). right isosceles triangle

Answer 1

Hint: We have to find the coordinates of the points $S$, \[U\] and \[V\], for which the equation of a tangent to the parabola given by $yt=x+a{{t}^{2}}$ would be required.

Complete step-by-step solution -

In the question, the equation of the parabola is given as ${{y}^{2}}=4ax$. The tangent at a point $P$ is said to meet the directrix at point $U$ and the base of latus rectum at $V$.
The directrix of the parabola of the form ${{y}^{2}}=4ax$ is given by $x=-a$. The latus rectum is given by $x=a$. The focus, $S$ of the parabola is $\left( a,0 \right)$. Also, we know that the latus rectum passes through the focus.
The coordinates of the tangent at point $P$ on the parabola can be taken in the parametric form as $\left( a{{t}^{2}},2at \right)$.
The figure showing all these details can be drawn as below,


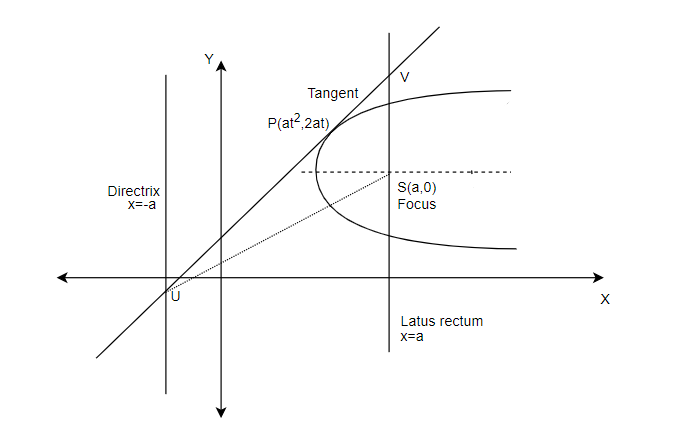
We know that the equation of a tangent to the parabola is given by,
$yt=x+a{{t}^{2}}\ldots \ldots \ldots \left( i \right)$
We have to find the coordinates of the points $U$ and $V$.
Since the point $U$ lies on the directrix, it is clear that it will have the $x$ coordinate as $-a$, so the $y$ coordinate can be obtained by substituting $x=-a$ in equation $\left( i \right)$,
$\begin{align}
  & yt=-a+a{{t}^{2}} \\
 & y=\dfrac{-a+a{{t}^{2}}}{t} \\
\end{align}$
Therefore, the coordinates of point $U$ are $\left( -a,\dfrac{-a+a{{t}^{2}}}{t} \right)$.
Since the point $V$ lies on the latus rectum, it is clear that it will have the $x$ coordinate as $a$, so the $y$ coordinate can be obtained by substituting $x=a$ in equation $\left( i \right)$,
$\begin{align}
  & yt=a+a{{t}^{2}} \\
 & y=\dfrac{a+a{{t}^{2}}}{t} \\
\end{align}$
Therefore, the coordinates of point $V$ are $\left( a,\dfrac{a+a{{t}^{2}}}{t} \right)$.
Looking at the options, it is clear that we have to find what type of triangle is formed by $SUV$. For which we will have to compute the length of the sides $SU,SV$ and $UV$.
The distance formula is used for finding the length. For two points with coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, it is given by,
$D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
So, we can find the length of $SU$ with coordinates $\left( a,0 \right)$ and $\left( -a,\dfrac{-a+a{{t}^{2}}}{t} \right)$ as
$\begin{align}
  & SU=\sqrt{{{\left( -a-a \right)}^{2}}+{{\left( \dfrac{-a+a{{t}^{2}}}{t}-0 \right)}^{2}}} \\
 & SU=\sqrt{{{\left( -2a \right)}^{2}}+{{\left( \dfrac{-a+a{{t}^{2}}}{t} \right)}^{2}}} \\
 & SU=\sqrt{4{{a}^{2}}+\dfrac{{{\left( -a+a{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
\end{align}$
Taking $a$ outside from the numerator of the second term, we get
$\begin{align}
  & SU=\sqrt{4{{a}^{2}}+\dfrac{{{\left( a\left( -1+{{t}^{2}} \right) \right)}^{2}}}{{{t}^{2}}}} \\
 & SU=\sqrt{4{{a}^{2}}+\dfrac{{{a}^{2}}{{\left( -1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
\end{align}$
Taking the common term ${{a}^{2}}$ outside the root, we get
$SU=a\sqrt{4+\dfrac{{{\left( -1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}}$
Taking the LCM and simplifying, we get
$\begin{align}
  & SU=a\sqrt{\dfrac{4{{t}^{2}}+{{\left( -1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
 & SU=a\sqrt{\dfrac{4{{t}^{2}}+1+{{t}^{4}}-2{{t}^{2}}}{{{t}^{2}}}} \\
 & SU=a\sqrt{\dfrac{1+{{t}^{4}}+2{{t}^{2}}}{{{t}^{2}}}} \\
\end{align}$
Since we know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$, we can simplify as
$\begin{align}
  & SU=a\sqrt{\dfrac{{{\left( 1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
 & SU=a\dfrac{\left( 1+{{t}^{2}} \right)}{t}\ldots \ldots \ldots \left( ii \right) \\
\end{align}$
Now, we can get the length of $SV$ with coordinates $\left( a,0 \right)$ and $\left( a,\dfrac{a+a{{t}^{2}}}{t} \right)$ as
\[\begin{align}
  & SV=\sqrt{{{\left( a-a \right)}^{2}}+{{\left( \dfrac{a+a{{t}^{2}}}{t}-0 \right)}^{2}}} \\
 & SV=\sqrt{{{0}^{2}}+{{\left( \dfrac{a+a{{t}^{2}}}{t} \right)}^{2}}} \\
 & SV=\sqrt{\dfrac{{{\left( a+a{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
\end{align}\]
Taking the term ${{a}^{2}}$ outside from the numerator,
\[\begin{align}
  & SV=\sqrt{\dfrac{{{a}^{2}}{{\left( 1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}}} \\
 & SV=\dfrac{a\left( 1+{{t}^{2}} \right)}{t}\ldots \ldots \ldots \left( iii \right) \\
\end{align}\]
The length of $UV$ with coordinates $\left( -a,\dfrac{-a+a{{t}^{2}}}{t} \right)$ and $\left( a,\dfrac{a+a{{t}^{2}}}{t} \right)$ is
$\begin{align}
  & UV=\sqrt{{{\left( a+a \right)}^{2}}+{{\left( \dfrac{a+a{{t}^{2}}}{t}-\dfrac{-a+a{{t}^{2}}}{t} \right)}^{2}}} \\
 & UV=\sqrt{{{\left( 2a \right)}^{2}}+{{\left( \dfrac{a+a{{t}^{2}}+a-a{{t}^{2}}}{t} \right)}^{2}}} \\
 & UV=\sqrt{{{\left( 2a \right)}^{2}}+{{\left( \dfrac{2a}{t} \right)}^{2}}} \\
 & UV=\sqrt{{{\left( 2a \right)}^{2}}+\dfrac{{{\left( 2a \right)}^{2}}}{{{t}^{2}}}} \\
\end{align}$
Taking out the common term ${{\left( 2a \right)}^{2}}$ outside the root,
$UV=2a\sqrt{1+\dfrac{1}{{{t}^{2}}}}\ldots \ldots \ldots \left( iv \right)$
From equations $\left( ii \right)$ and $\left( iii \right)$, we get that $SU=SV$. The side $UV$ is different from the other sides. Since two sides of the triangle are equal, it can be an isosceles triangle.
To check if it is a right isosceles triangle, we have to apply the Pythagoras theorem,
$U{{V}^{2}}=S{{U}^{2}}+S{{V}^{2}}$
Since we know that$SU=SV$,
$U{{V}^{2}}=2S{{U}^{2}}$
Substituting the values, we get
$\begin{align}
  & {{\left[ 2a\sqrt{1+\dfrac{1}{{{t}^{2}}}} \right]}^{2}}=2{{\left[ \dfrac{a\left( 1+{{t}^{2}} \right)}{t} \right]}^{2}} \\
 & 4{{a}^{2}}\left( 1+\dfrac{1}{{{t}^{2}}} \right)\ne 2{{a}^{2}}\dfrac{{{\left( 1+{{t}^{2}} \right)}^{2}}}{{{t}^{2}}} \\
\end{align}$
Since both sides are not equal, it does not satisfy the Pythagoras theorem and is not a right isosceles triangle.
Therefore, we get that the triangle formed by points $SUV$ is an isosceles triangle.
Hence, the correct answer is option (c).

Note: Whenever we get this type of question, the first step is to find the coordinates of the points that form the shape, in this case, the triangle. The equation of the tangent must be known to solve this question. Once we have the coordinates, the length can be computed and the answer can be obtained. Another point to keep in mind is to simplify the lengths obtained to the simplest form and then check if they are equal or not.