
The value of electric potential at any point due to any electric dipole is:-
A.
B.
C.
D.
Answer
147k+ views
Hint:The electric dipole is a system of two charges that are separated by a finite distance. The dipole has a property called dipole moment which is equal to the product of the charges and the distance of separation between them. To find the value of electric potential at any point due to any electric dipole we use electric potential due to both charges.
Formula used: >
The potential due to this dipole is given as
Where p is dipole moment, r is distance from dipole, k is coulomb’s constant,
Dipole moment is given as,
Where q is the charge and 2l is the distance of two charges.
Complete step by step solution:
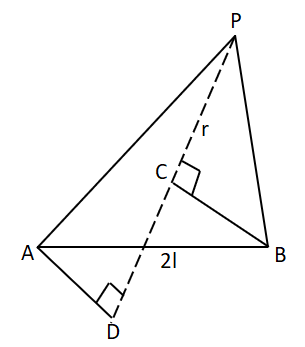
Image: A point P is at some distance r from the dipole.
In figure AB the dipole of distance between them is 2l. Point P is at a distance r from the midpoint of AB.
BP=CP=OP-OC=
AP=DP=OP-OD=
Electric potential due to -q,
Electric potential due to +q,
Now electric potential at P can be:
As distance between the dipoles are less, so we can write;
Also we know that
By using these values in above, we get
Therefore the value of electric potential at any point due to any electric dipole is
Hence option D is the correct answer.
Note: As we know electric dipoles consist of two charges equal in magnitude (q) but opposite in nature one is a positive charge and other is a negative charge. These two charges are separated by a distance. Electric potential obeys superposition principle due to electric dipoles as a whole can be sum of potential due to both the charges positive and negative.
Formula used: >
The potential due to this dipole is given as
Where p is dipole moment, r is distance from dipole, k is coulomb’s constant,
Dipole moment is given as,
Where q is the charge and 2l is the distance of two charges.
Complete step by step solution:

Image: A point P is at some distance r from the dipole.
In figure AB the dipole of distance between them is 2l. Point P is at a distance r from the midpoint of AB.
BP=CP=OP-OC=
AP=DP=OP-OD=
Electric potential due to -q,
Electric potential due to +q,
Now electric potential at P can be:
As distance between the dipoles are less, so we can write;
Also we know that
By using these values in above, we get
Therefore the value of electric potential at any point due to any electric dipole is
Hence option D is the correct answer.
Note: As we know electric dipoles consist of two charges equal in magnitude (q) but opposite in nature one is a positive charge and other is a negative charge. These two charges are separated by a distance. Electric potential obeys superposition principle due to electric dipoles as a whole can be sum of potential due to both the charges positive and negative.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Ideal and Non-Ideal Solutions Raoult's Law - JEE

A proton accelerated by a potential difference of 500 class 12 physics JEE_Main

Charging and Discharging of Capacitor

Other Pages
JEE Advanced Study Plan for 2025: Tips, Timetable, and Strategy

Collision - Important Concepts and Tips for JEE

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Explain the construction and working of a GeigerMuller class 12 physics JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

JEE Advanced Live Classes for 2025 By Vedantu




