
The value of ‘g’ on the surface of the earth is
A. Maximum at poles
B. Maximum at equator
C. Same everywhere
D. Minimum at poles
Answer
147k+ views
Hint: Solution can be found by observing the gravitational attraction formula, where gravitational force is inversely proportional to the distance from the center of the earth. Thus, extending it to the concept that Earth is not a perfect sphere and the distance of poles and the equator is different from the center of earth.
Complete step-by-step answer:
Gravitational attractive force felt by a body on the earth’s surface is given as;
G is the gravitational constant
r is the distance from the earth’s center
M is the mass of the earth
M is the mass of the body.
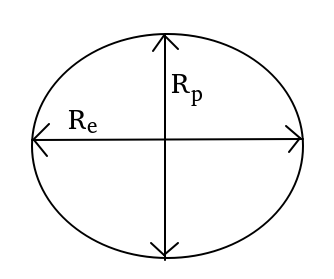
We can observe from the above image that earth is not a perfect sphere. It is slightly bulged at the equator, and flattened at the poles. Thus, from the above diagram we can observe that;
where,
We know from the gravitational attraction and thus the acceleration due to gravity ‘g’ becomes:
Thus, for poles:
Thus, for equator:
So, since
Therefore, the correct answer to this question is option A. That is ‘g’ is maximum at poles.
Note: The gravitational force is an attractive force that is, it always attracts and never repels. It never pushes two masses further, only a pulling force is generated. The ‘g’ is the acceleration of gravity and is equal to
Complete step-by-step answer:
Gravitational attractive force felt by a body on the earth’s surface is given as;
G is the gravitational constant
r is the distance from the earth’s center
M is the mass of the earth
M is the mass of the body.

We can observe from the above image that earth is not a perfect sphere. It is slightly bulged at the equator, and flattened at the poles. Thus, from the above diagram we can observe that;
where,
We know from the gravitational attraction and thus the acceleration due to gravity ‘g’ becomes:
Thus, for poles:
Thus, for equator:
So, since
Therefore, the correct answer to this question is option A. That is ‘g’ is maximum at poles.
Note: The gravitational force is an attractive force that is, it always attracts and never repels. It never pushes two masses further, only a pulling force is generated. The ‘g’ is the acceleration of gravity and is equal to
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Ideal and Non-Ideal Solutions Raoult's Law - JEE

A solid cube and a solid sphere of the same material class 11 physics JEE_Main

A boy wants to throw a ball from a point A so as to class 11 physics JEE_Main

Other Pages
Laws of Motion Class 11 Notes: CBSE Physics Chapter 4

Which of the following is used as a coolant in an automobile class 11 physics JEE_Main

Charging and Discharging of Capacitor

Select incorrect statements A Zero acceleration of class 11 physics JEE_Main

The graph shows the variation of displacement of a class 11 physics JEE_Main

JEE Advanced Study Plan for 2025: Tips, Timetable, and Strategy




