
The voltage across the
Answer
142.8k+ views
Hint: In order to proceed with the problem first we need to know about ohm’s law. It states that the voltage across a conductor is directly proportional to the current flowing through it.
Formula Used:
To find the equation for voltage we have,
Where, I is current and R is resistance.
Complete step by step solution:
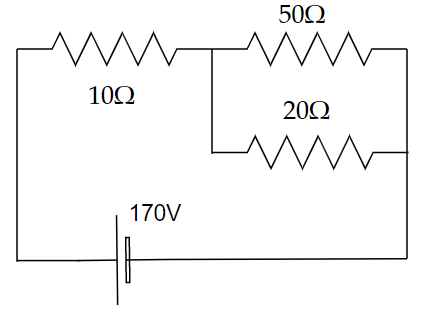
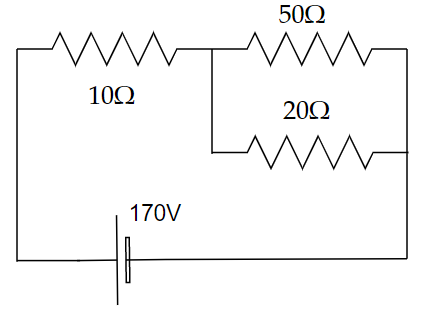
Image: A circuit consists of three resistors and a battery.
In the above circuit, the voltage across the
In order to find the current in the circuit, we need to simplify the given circuit by finding the equivalent resistance of the two resistors given in a parallel combination.
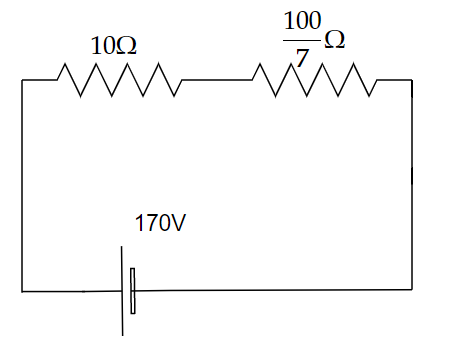
Image: An equivalent resistor.
The equivalent resistance is given by,
Here,
Substitute the value in the above equation we get,
Then,
Here,
Then the above equation will become,
Using Ohm’s law,
Now substitute the value of V and R in the above equation we get,
Now, in order to find the voltage across
Therefore, the value of x is 70.
Note:Here it is important to remember that, in a circuit when two are more resistors are connected in parallel, we need to apply equivalent resistance formula as
Formula Used:
To find the equation for voltage we have,
Where, I is current and R is resistance.
Complete step by step solution:

Image: A circuit consists of three resistors and a battery.
In the above circuit, the voltage across the
In order to find the current in the circuit, we need to simplify the given circuit by finding the equivalent resistance of the two resistors given in a parallel combination.

Image: An equivalent resistor.
The equivalent resistance is given by,
Here,
Substitute the value in the above equation we get,
Then,
Here,
Then the above equation will become,
Using Ohm’s law,
Now substitute the value of V and R in the above equation we get,
Now, in order to find the voltage across
Therefore, the value of x is 70.
Note:Here it is important to remember that, in a circuit when two are more resistors are connected in parallel, we need to apply equivalent resistance formula as
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
EMI starts from ₹2,775 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Physics Average Value and RMS Value JEE Main 2025

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




