Question

What should be the width of each slit to obtain $10$ maxima of double slit interference pattern within the central maximum of single slit diffraction pattern?

Answer 1

Hint: This is a complicated question the students should have a deep knowledge on the single and double slit experiment to understand the question. We should know about the relation between the double and single slit experiment so that we can understand the question properly.

Complete step by step answer
Single slit diffraction: Single slit diffraction occurs in a single slit experiment where light waves from a source passes through a single slit of width ‘w’ which is in the order of the wavelength of the light wave passing through it to get a distinctive pattern called diffraction pattern.
Double slit experiment: double slit diffraction occurs in a when where light waves from a source passes through a two slits of width ‘w’ which is in the order of the wavelength of the light wave passing through it to get a diffraction pattern.
When the double slit in Young’s experiment is replaced by a single narrow slit (illuminated by a monochromatic source), a broad pattern with a central bright region is observed. On both sides, there are alternate dark and bright regions, the intensity becoming weaker away from the centre the angular size of the central maximum increases when the slit width decreases. The double-slit experiment, is actually a superposition of single-slit diffraction from each slit or hole.




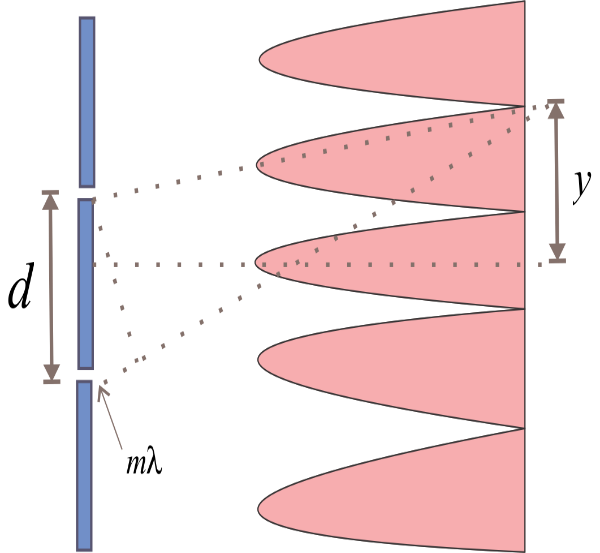
                      Single slit experiment Double slit experiment

In the diagram,
a and d are the width of the slit.
y is the central maximum.
The angular width of the central maximum of single slit diffraction is $2\theta = \dfrac{{2\lambda }}{a}$
Where,
$\lambda $ is the wavelength
$a$ is the width of the slit
The angular width of the central maximum of double slit diffraction is $2\theta = \dfrac{\lambda }{d}$
$\lambda $ is the wavelength
$d$ is the width of the slit
The angular width of the central maximum of single slit diffraction is $2\theta = \dfrac{{2\lambda }}{a}{\text{ }} \to {\text{1}}$
Width of each slit to obtain $10$ maxima of double slit interference pattern within the central maximum of single slit diffraction pattern $ \Rightarrow 2\theta = 10 \times \dfrac{\lambda }{d}{\text{ }} \to {\text{2}}$


The double slit interference pattern of 10 maxima (The envelope shows the single slit experiment)

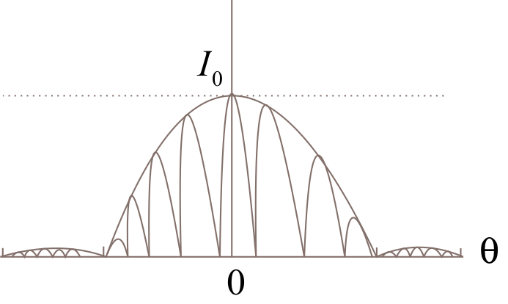
We have to find the width of each slit to obtain $10$ maxima of double slit interference pattern within the central maximum of single slit diffraction pattern.
Equate 1 and 2
$ \Rightarrow \dfrac{{2\lambda }}{a} = 10 \times \dfrac{\lambda }{d}$
$ \Rightarrow a = \dfrac{d}{5}$
$a$ is the width of the single slit.
$d$ is the width of the double slit.
We have to find the width of both single and double slit which have the same width.
So, let us take the width of slit as $a$ in common.
$ \Rightarrow a = \dfrac{1}{5}$
$ \Rightarrow a = 0.2mm$

Note: Students should be aware that here the width of the slit is written in millimetres. Generally we write the measurement of slit width in millimetres, we follow the same when we do the problem.