
Three mediums of refractive indices ${\mu _1},{\mu _0}{\text{ and }}{\mu _2}$ are shown in the fig. $\left( {{\mu _1} > {\mu _0},{\text{ and }}{\mu _2} > {\mu _0}} \right)$. The lamps $A$ and $B$ are placed at the bottom and top of the first and third mediums of the same thickness. If the bottom layer of the middle medium is illuminated for a circle of half of the radius for which the upper layer of this medium is illuminated, the relationship between ${\mu _1}{\text{ and }}{\mu _2}$ is $\left( {given{\text{ }}{\mu _0} = 1} \right)$:

$\left( a \right){\text{ 2}}{\mu _2} = \sqrt {\mu _1^2 + 3} $
$\left( b \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 4} $
$\left( c \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 2} $
$\left( d \right){\text{ }}{\mu _2} = \sqrt {\mu _1^2 + 1} $
Answer
122.7k+ views
Hint First of all by using the formula which is $\operatorname{Sin} c = \dfrac{1}{\mu }$and from this we can now calculate the $\tan {c_1}$ and similarly we will calculate $\tan {c_2}$ and from this we will calculate the radius and them by morphing the distance $r$, we will get the relation between ${\mu _1}{\text{ and }}{\mu _2}$.
Formula used:
By using Snell’s law
$\operatorname{Sin} c = \dfrac{1}{\mu }$, and
$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$
Here, $\mu $ will be the refractive index.
Complete step by step solution
First of all, we will make the figure from the question and elaborate the figure. Here, by using the Pythagoras theorem we will mark the positions and find the angle between them. The height will be the same in both the mediums.
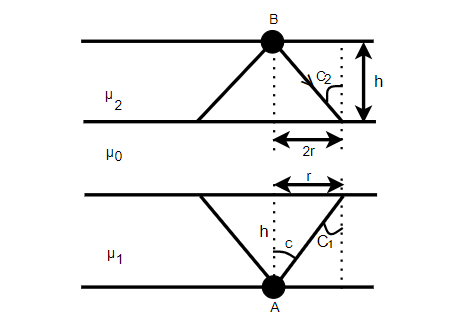
On elaborating the figure, by using the formula $\operatorname{Sin} c = \dfrac{1}{\mu }$and$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$.
Therefore by using the above, we get
$\tan {c_1} = \dfrac{r}{h}$
And here from the $r$will be given as
$ \Rightarrow r = h\tan {c_1}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$ \Rightarrow r = h \times \dfrac{1}{{\sqrt {\mu _1^2 - 1} }}$, we will let it equation $1$
Now also $\tan {c_2} = \dfrac{{2r}}{h}$
And here from the $r$will be given as
$ \Rightarrow 2r = h\tan {c_2}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$ \Rightarrow 2r = h \times \dfrac{1}{{\sqrt {\mu _2^2 - 1} }}$, we will let it equation $2$
Now on dividing the equation $1$and equation$2$, we get
$ \Rightarrow \dfrac{1}{2} = \dfrac{{\sqrt {\mu _2^2 - 1} }}{{\sqrt {\mu _1^2 - 1} }}$
Now on squaring both the sides, we get
$ \Rightarrow \dfrac{1}{4} = \dfrac{{\mu _2^2 - 1}}{{\mu _1^2 - 1}}$
So on doing the cross-multiplication, we get
$ \Rightarrow \mu _1^2 - 1 = 4\mu _2^2 - 4$
And solving the above equation by removing the square, we get
$ \Rightarrow 2{\mu _2} = \sqrt {\mu _1^2 + 3} $
Therefore, the relation between ${\mu _1}{\text{ and }}{\mu _2}$is$2{\mu _2} = \sqrt {\mu _1^2 + 3} $.
Hence, the option $\left( a \right)$is correct.
Note As we have seen that there is a very little bit of concept used for solving this question. The question more emphasizes the calculation and by using the properties of the refraction, we can answer it easily. We just have to use some Pythagoras rule and some trigonometric formulas to solve this.
Formula used:
By using Snell’s law
$\operatorname{Sin} c = \dfrac{1}{\mu }$, and
$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$
Here, $\mu $ will be the refractive index.
Complete step by step solution
First of all, we will make the figure from the question and elaborate the figure. Here, by using the Pythagoras theorem we will mark the positions and find the angle between them. The height will be the same in both the mediums.

On elaborating the figure, by using the formula $\operatorname{Sin} c = \dfrac{1}{\mu }$and$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$.
Therefore by using the above, we get
$\tan {c_1} = \dfrac{r}{h}$
And here from the $r$will be given as
$ \Rightarrow r = h\tan {c_1}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$ \Rightarrow r = h \times \dfrac{1}{{\sqrt {\mu _1^2 - 1} }}$, we will let it equation $1$
Now also $\tan {c_2} = \dfrac{{2r}}{h}$
And here from the $r$will be given as
$ \Rightarrow 2r = h\tan {c_2}$
Now by substituting the value$\tan c = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}$, we get
$ \Rightarrow 2r = h \times \dfrac{1}{{\sqrt {\mu _2^2 - 1} }}$, we will let it equation $2$
Now on dividing the equation $1$and equation$2$, we get
$ \Rightarrow \dfrac{1}{2} = \dfrac{{\sqrt {\mu _2^2 - 1} }}{{\sqrt {\mu _1^2 - 1} }}$
Now on squaring both the sides, we get
$ \Rightarrow \dfrac{1}{4} = \dfrac{{\mu _2^2 - 1}}{{\mu _1^2 - 1}}$
So on doing the cross-multiplication, we get
$ \Rightarrow \mu _1^2 - 1 = 4\mu _2^2 - 4$
And solving the above equation by removing the square, we get
$ \Rightarrow 2{\mu _2} = \sqrt {\mu _1^2 + 3} $
Therefore, the relation between ${\mu _1}{\text{ and }}{\mu _2}$is$2{\mu _2} = \sqrt {\mu _1^2 + 3} $.
Hence, the option $\left( a \right)$is correct.
Note As we have seen that there is a very little bit of concept used for solving this question. The question more emphasizes the calculation and by using the properties of the refraction, we can answer it easily. We just have to use some Pythagoras rule and some trigonometric formulas to solve this.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Mains 2025: Check Important Dates, Syllabus, Exam Pattern, Fee and Updates

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Chemistry Exam Pattern 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main




