Question

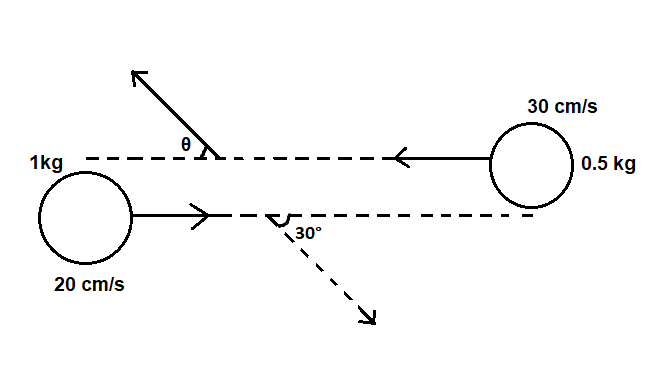
Two balls collide bounce off each other as shown in the figure. The \[1kg\] ball has a speed $10cm/s$ after collision. The velocity of the $0.5kg$ ball will be

(A) $36cm/s$
(B) $24cm/s$
(C) $12.4cm/s$
(D) $18cm/s$

Answer 1

Hint According to Newton’s second law of motion, the rate of change of momentum of a body is directly proportional to the applied force and the change takes place in the direction of the force. We know that the momentum of a body is equal to the product of mass and velocity. So if we calculate the momentum we can find the velocity from that.
Formula used:
$P = mv$ (Where $P$ stands for the momentum of the object, $m$stands for the mass of the object, and $v$ stands for the velocity of the particle.)

Complete Step by step solution

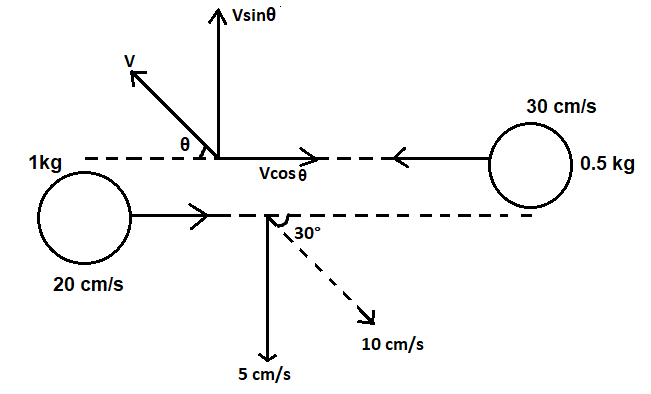
The figure given above shows how we can resolve the velocity vector into its components.
After the collision, the $1kg$ball will have a velocity $10cm/s$
The angle between the velocity vector and the path of the ball is given as, ${30^ \circ }$
From this, we can find the sin component of the velocity vector of$1kg$the ball as,
$v\sin \theta = 10\sin {30^ \circ } = 5cm/s$
Let us take the velocity of the $0.5kg$as $v$ and the sin and cos components of the velocity vector are $v\sin \theta $and $v\cos \theta $respectively.
According to the principle of conservation of linear momentum,
The momentum along the $y$direction will be,
${P_i} = {P_f} = 0$…………………………………………………………………(1)
Where ${P_i}$ is the initial momentum and ${P_f}$is the final momentum
We know that the momentum of a body is,
$P = mv$
Substituting the values of mass and the component of velocity in $y$direction in the equation (1)
$1 \times 5 = \left( {0.5} \right)v\sin \theta = 0$
From this equation, we can write
$5 - \left( {0.5} \right)v\sin \theta = 0$
We can write
$v\sin \theta = \dfrac{5}{{0.5}} = 10cm/s$
From this, we get that
 $v\sin \theta = 10cm/s$…………………………………………………………………………………..(2)
The momentum of the body in $x$-direction is,
${P_i} = {P_f}$
i.e.
${m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1}\cos \theta + {m_2}{v_2}\cos \theta $………………………………………………………..(3)
It is given that,
${m_1} = 1kg$
${u_1} = 20cm/s$
${m_2} = 0.5kg$
${u_2} = 30cm/s$
${v_1}\cos \theta = 10\cos {30^ \circ } = 10\dfrac{{\sqrt 3 }}{2} = 5\sqrt 3 $
We have to find the value of ${v_2}$from equation (3)
Substituting the values in equation (2), we get
$1 \times 20 - 0.5 \times 30 = 1 \times 5\sqrt 3 - 0.5 \times {v_2}\cos \theta $
Calculating,
$20 - 15 = 5\sqrt 3 - 0.5v\cos \theta $
$5\sqrt 3 - 5 = 0.5v\cos \theta $
From this we get
$v\cos \theta = \dfrac{{5(\sqrt 3 - 1)}}{{0.5}} = 10\left( {\sqrt 3 - 1} \right)$
We can write
$v\cos \theta = 10\left( {\sqrt 3 - 1} \right)$………………………………………………………………….(4)
Squaring and add equation (2) and (4)
${v^2}{\sin ^2}\theta + {v^2}{\cos ^2}\theta = {10^2} + {\left( {10\left( {\sqrt 3 - 1} \right)} \right)^2}$
This can be written as,
${v^2}({\sin ^2}\theta + {\cos ^2}\theta ) = {10^2}\left( {1 + 3 + 1 - 2\sqrt 3 } \right)$
${v^2} = {10^2}\left( {5 - 2\sqrt 3 } \right)$ $\left( {\because {{\sin }^2}\theta + {{\cos }^2}\theta = 1} \right)$
We can get the velocity by taking the square root of the above equation,
$v = 10\sqrt {5 - 2\sqrt 3 } $
This will be,
$v = 10\sqrt {1.5358} $
i.e.
$v = 12.4cm/s$

The answer is:Option (C): $12.4cm/s$

Note
In all collisions the total linear momentum is conserved. But the kinetic energy of the system need not be conserved. The collision in which the total kinetic energy is conserved is called an elastic collision. If the total kinetic energy of a system is not conserved after collision then it is called an inelastic collision.