
Two blocks are in contact on a frictionless table. One has mass m and the other 2m a force F is applied on 2m as shown in the figure. Now the same force F is applied from the right on m. In the two cases respectively, the ratio of the force of contact between the two blocks will be:
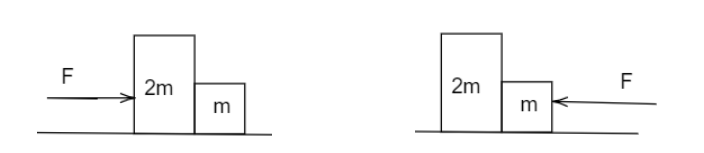
(A) same
(B)
(C)
(D)
Answer
143.1k+ views
Hint Due to the force of contact both the masses will move together with the same acceleration. Force of contact acting between the two blocks will be the driving force for the movement for block m (when force is acting from the left side) and 2m (when force is acting from the right side).
Formula used:
Complete Step-by-step solution
Let, case A be the case in which force is acting on the left side i.e. on block 2m and case B be the case in which force is acting on the right side i.e. on block m.
Due to the force of contact both the masses will move together with the same acceleration.
Hence,
Here, considering both the blocks as one system,
In case A force of contact will cause movement of the block of mass m.
In case B force of contact will cause movement of a block of mass 2m.
Let
We know that
So,
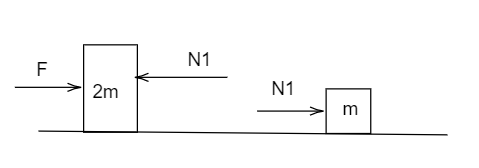
So,
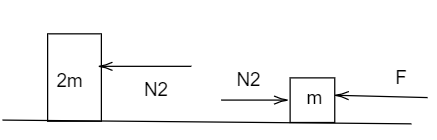
In the question they are asking ratio of
Note Above we solved considering the free body diagram of the body on which force of contact is acting but we can also solve it by considering the free body diagram of other body by balancing force on it and following
Formula used:
Complete Step-by-step solution
Let, case A be the case in which force is acting on the left side i.e. on block 2m and case B be the case in which force is acting on the right side i.e. on block m.
Due to the force of contact both the masses will move together with the same acceleration.
Hence,
Here, considering both the blocks as one system,
In case A force of contact will cause movement of the block of mass m.
In case B force of contact will cause movement of a block of mass 2m.
Let
We know that
So,

So,

In the question they are asking ratio of
Note Above we solved considering the free body diagram of the body on which force of contact is acting but we can also solve it by considering the free body diagram of other body by balancing force on it and following
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Electron Gain Enthalpy and Electron Affinity for JEE

Electrical Field of Charged Spherical Shell - JEE

Physics Average Value and RMS Value JEE Main 2025

Other Pages
JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Geostationary Satellites and Geosynchronous Satellites - JEE Important Topic

Charging and Discharging of Capacitor

The dimensional formula of k Coulombs Constant is Take class 11 physics JEE_Main

Collision - Important Concepts and Tips for JEE




