Question

Two bodies of masses $m$ and $M$ are placed at distance $d$ apart. What is the gravitational potential $\left( V \right)$ at the position where the gravitational field due to them zero is $V$ is:
(A) $V = - \dfrac{G}{d}\left( {m + M} \right)$
(B) $V = \dfrac{G}{d}m$
(C) $V = \dfrac{G}{d}M$
(D) \[V = - \dfrac{G}{d}{\left( {\sqrt m + \sqrt M } \right)^2}\]

Answer 1

Hint Two bodies of different masses m and M are placed at a distance d apart. We have to find the gravitational potential at that point where $g = 0$. It is given that at a particular point the gravitational field due to two bodies is zero so their gravitational field is equal at this point, so equate their gravitational field and find the distance of each body from the point where $g = 0$ so that we can use that distance value to find the net gravitational potential due to them.

Complete step by step answer
The gravitational field is defined as the gravitational force which is exerted on a mass at that point. For a body of mass M, the magnitude gravitational field at distance r is given by
$ \Rightarrow g = \dfrac{{GM}}{{{r^2}}}$
G is the gravitational constant
r is the distance
g is the gravitational field
M is the mass of the body
Given,
Two bodies of masses $m$ and $M$ are placed at distance $d$ apart
Let the distance between the point $g = 0$ and the mass m be $x$
Let the distance between the point $g = 0$ and the mass M be $d - x$
Let us draw a diagram to understand the concept


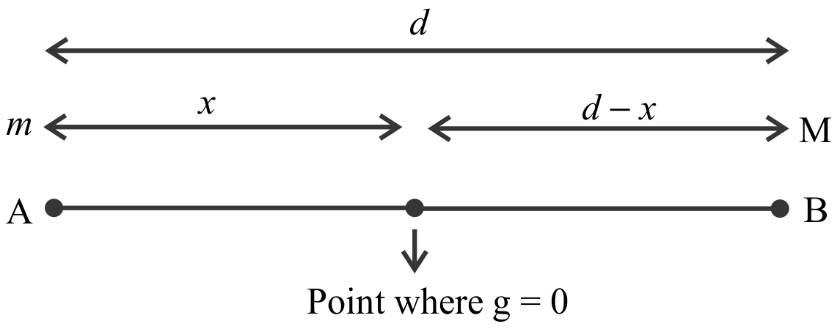
The gravitational field due to the mass m is
$ \Rightarrow {g_1} = \dfrac{{Gm}}{{{x^2}}}{\text{ }} \to {\text{1}}$
The gravitational field due to the mass M is
$ \Rightarrow {g_2} = \dfrac{{GM}}{{{{\left( {d - x} \right)}^2}}}{\text{ }} \to {\text{2}}$
At a particular point, the gravitational field is zero due to both the masses M and m
$ \Rightarrow {g_1} = {g_2} = 0$
Which means at that point where $g = 0$ the gravitational field due to mass M and m are equal
 $ \Rightarrow {g_1} = {g_2}$
$ \Rightarrow \dfrac{{Gm}}{{{x^2}}} = \dfrac{{GM}}{{{{\left( {d - x} \right)}^2}}}$
$ \Rightarrow \dfrac{m}{{{x^2}}} = \dfrac{M}{{{{\left( {d - x} \right)}^2}}}$
$ \Rightarrow \dfrac{{{{\left( {d - x} \right)}^2}}}{{{x^2}}} = \dfrac{M}{m}$
Taking square root on both sides
$ \Rightarrow \dfrac{{\left( {d - x} \right)}}{x} = \sqrt {\dfrac{M}{m}} {\text{ }} \to {\text{3}}$
$ \Rightarrow \dfrac{d}{x} - 1 = \sqrt {\dfrac{M}{m}} $
$ \Rightarrow \dfrac{d}{x} = 1 + \sqrt {\dfrac{M}{m}} $
$ \Rightarrow \dfrac{d}{x} = \dfrac{{\sqrt m + \sqrt M }}{{\sqrt m }}$
$ \Rightarrow x = \dfrac{{\sqrt m }}{{\sqrt m + \sqrt M }} \times d{\text{ }} \to {\text{4}}$
Now take the equation 3
$ \Rightarrow \dfrac{{\left( {d - x} \right)}}{x} = \sqrt {\dfrac{M}{m}} $
This can be written as
$ \Rightarrow d - x = \sqrt {\dfrac{M}{m}} \times x$
Substitute the value of x from equation 4
$ \Rightarrow d - x = \dfrac{{\sqrt M }}{{\sqrt m }} \times \dfrac{{\sqrt m }}{{\sqrt m + \sqrt M }} \times d$
$ \Rightarrow d - x = \dfrac{{\sqrt M }}{{\sqrt m + \sqrt M }} \times d{\text{ }} \to {\text{5}}$
Now equation 4 and 5 gives the value of $x{\text{ and d - x}}$
We have to find the gravitational potential $\left( V \right)$ at the position $V$where the gravitational field is zero
Gravitational potential is defined as the potential energy which unit mass would have at any point.
The gravitational potential $\left( V \right)$ is given by
$ \Rightarrow V = - \dfrac{{GM}}{r}$
V is the gravitational potential
G is the gravitational constant
r is the distance
M is the mass of the body
The gravitational potential due to mass m is
$ \Rightarrow {V_1} = - \dfrac{{Gm}}{x}$
The gravitational potential due to mass m is
$ \Rightarrow {V_2} = - \dfrac{{GM}}{{d - x}}$
The net gravitational potential due to the two masses at the point where gravitational field is zero, $g = 0$ is
$ \Rightarrow V = {V_1} + {V_2}$
\[ \Rightarrow V = - \dfrac{{Gm}}{x} + \left( { - \dfrac{{GM}}{{d - x}}} \right)\]
Substitute the values of x and d-x
\[ \Rightarrow V = - \dfrac{{Gm}}{{\dfrac{{\sqrt m }}{{\sqrt m + \sqrt M }} \times d}} - \dfrac{{GM}}{{\dfrac{{\sqrt M }}{{\sqrt m + \sqrt M }} \times d}}\]
\[ \Rightarrow V = - \dfrac{{\left( {\sqrt m + \sqrt M } \right)Gm}}{{\sqrt m d}} - \dfrac{{\left( {\sqrt m + \sqrt M } \right)GM}}{{\sqrt M d}}\]
\[ \Rightarrow V = \left( { - \dfrac{{\left( {\sqrt m + \sqrt M } \right)Gm \times \sqrt M }}{{\sqrt M \sqrt m d}}} \right) - \left( {\dfrac{{\left( {\sqrt m + \sqrt M } \right)GM \times \sqrt m }}{{\sqrt m \sqrt M d}}} \right)\]
\[ \Rightarrow V = - \dfrac{G}{{d\sqrt M \sqrt m }}\left( {\left( {\sqrt m + \sqrt M } \right)m \times \sqrt M + \left( {\sqrt m + \sqrt M } \right)M \times \sqrt m } \right)\]
\[ \Rightarrow V = - \dfrac{G}{{d\sqrt M \sqrt m }}\left( {m\sqrt M \sqrt m + Mm + mM + M\sqrt m \sqrt M } \right)\]
\[ \Rightarrow V = - \dfrac{G}{{d\sqrt M \sqrt m }}\left( {m\sqrt M \sqrt m + \sqrt M \sqrt M \sqrt m \sqrt m + \sqrt m \sqrt m \sqrt M \sqrt M + M\sqrt m \sqrt M } \right)\]
\[ \Rightarrow V = - \dfrac{{G\sqrt m \sqrt M }}{{d\sqrt M \sqrt m }}\left( {m + \sqrt m \sqrt M + \sqrt m \sqrt M + M} \right)\]
\[ \Rightarrow V = - \dfrac{G}{d}\left( {m + M + 2\sqrt m \sqrt M } \right)\]
\[ \Rightarrow V = - \dfrac{G}{d}{\left( {\sqrt m + \sqrt M } \right)^2}\]

Hence the correct answer is option D) \[V = - \dfrac{G}{d}{\left( {\sqrt m + \sqrt M } \right)^2}\]

Note This problem looks difficult because of the calculation. But if you work it out, you can understand that this problem is an easy one. We have used only two basic formulas in this problem and we directly substituted the values without modifying the formula.