Question

Two cars are travelling on a straight road. The car ${{\text{C}}_1}$ is going at a constant speed of $9{\text{m}}{{\text{s}}^{ - 1}}$ . $40{\text{m}}$ ahead of ${{\text{C}}_1}$ is the car ${{\text{C}}_2}$ at rest, but starts moving with an acceleration of $1{\text{m}}{{\text{s}}^{ - 2}}$.
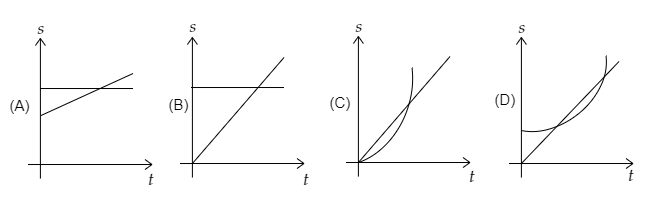
Which of the following graphs correctly represent the position of the two cars with time w.r.t the initial position of ${{\text{C}}_1}$ ?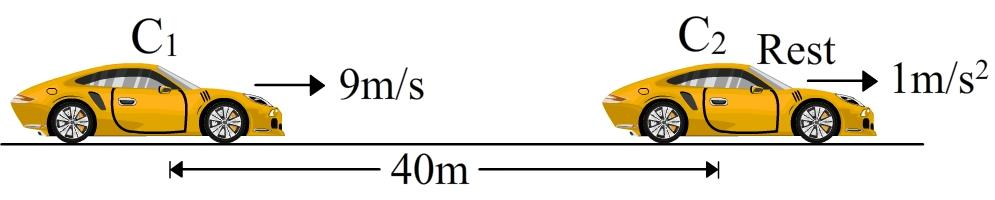

Answer 1

Hint: Here we can first obtain an equation for the distance $s$ covered by each car for the same time using Newton’s first equation of motion which is a relation connecting the distance covered by the car, the time taken, its initial velocity and its acceleration. Then based on these obtained equations we can sketch the required position versus time graph for the two cars. The required position-time graph is the one with respect to the initial position of ${{\text{C}}_1}$ .

Formula used:
Newton’s first equation of motion gives the distance covered by a body as $s = ut + \dfrac{1}{2}a{t^2}$ where $u$ is the initial velocity of the body, $t$ is the time taken and $a$ is the acceleration of the body.

Complete step by step solution:
List the known parameters of the two cars ${{\text{C}}_1}$ and ${{\text{C}}_2}$.
The initial constant velocity of the car ${{\text{C}}_1}$ is given to be ${u_1} = 9{\text{m}}{{\text{s}}^{ - 1}}$.
Since the car ${{\text{C}}_2}$ is at rest initially, its initial velocity will be zero i.e, ${u_2} = 0$ .
The acceleration of the car ${{\text{C}}_2}$ is given to be ${a_2} = 1{\text{m}}{{\text{s}}^{ - 2}}$.
The distance of separation between the two cars is given to be $40{\text{m}}$ .
Let ${s_1}$ and ${s_2}$ be the distance covered by cars ${{\text{C}}_1}$ and ${{\text{C}}_2}$ respectively in time $t$.
Using Newton’s first equation of motion, express the distance covered by the two cars in a time $t$.
Newton’s first equation of motion gives the distance covered by car ${{\text{C}}_1}$ as
${s_1} = {u_1}t = 9t$
Thus the equation for the position of the car ${{\text{C}}_1}$ is obtained as ${s_1} = 9t$ -------- (1)
Equation (1) represents a straight line. So the position versus time graph of ${{\text{C}}_1}$ w.r.t its initial position will be a straight line.
Now Newton’s first equation of motion gives the distance covered by car ${{\text{C}}_2}$ as
${s_2} = {u_2}t + \dfrac{1}{2}{a_2}{t^2} = \dfrac{{{t^2}}}{2}$
Thus the equation for the position of the car ${{\text{C}}_2}$ is obtained as ${s_2} = \dfrac{{{t^2}}}{2}$ . However, when the car ${{\text{C}}_1}$ was in motion ${{\text{C}}_2}$ remained at rest till the distance between the two cars was $40{\text{m}}$ . So when we consider the position of ${{\text{C}}_2}$ w.r.t the initial position of ${{\text{C}}_1}$ we have to take into account this initial distance of separation between the two cars.
Thus the equation for the position of the car ${{\text{C}}_2}$ w.r.t the initial position of ${{\text{C}}_1}$ will be
${s_{21}} = \dfrac{{{t^2}}}{2} + 40$ --------- (2)
Equation (2) represents a parabola.
So the position-time graph for the two cars w.r.t the initial position of ${{\text{C}}_1}$ will take the form given below.

So the correct option is D.

Note: Here the car ${{\text{C}}_1}$ is mentioned to be travelling at a constant speed. So its acceleration will be zero i.e., ${a_1} = 0$ . Thus we obtain the distance covered as that given by equation (1). In equation (1) when $t = 0{\text{s}}$ we have ${s_1} = 0{\text{m}}$ . So the straight line representing the position of ${{\text{C}}_1}$ will start at the origin. In equation (2), when $t = 0{\text{s}}$ we have ${s_{21}} = 40{\text{m}}$ so the parabola representing the position of ${{\text{C}}_2}$ will not start at the origin.