Question

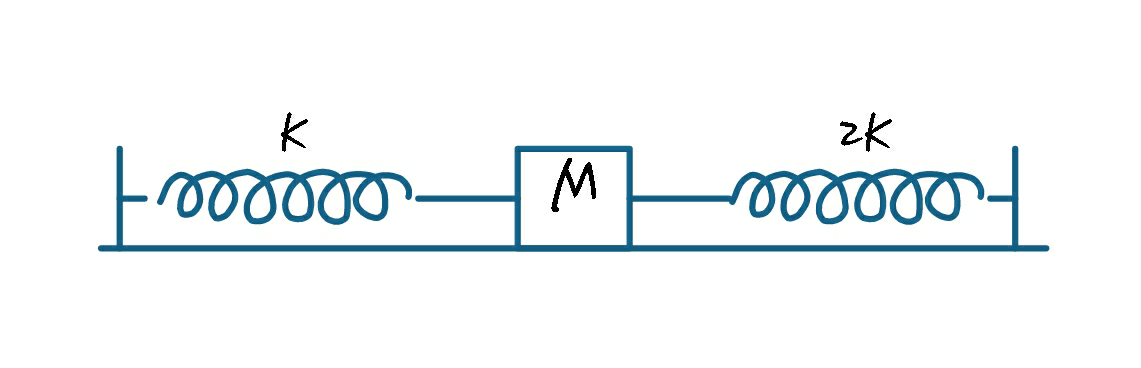
Two springs are connected in series and the combination is pulled by a constant force. If spring constant of two springs are $ $K\text{ and 2}K$ , then the ratio of potential energy stored in the springs is

Answer 1

Hint We know that PE is the amount of energy started at the highest point.
Here, two springs are converted in series
Therefore, using $P.E=\dfrac{1}{2}{{K}_{2}}$

Complete Step by Step Solution
$2:1$
For spring ${{S}_{1}}\text{ the spring constant is }K$
For spring${{S}_{2}}$ the spring constant is $2K$
Now, applying the potential energy formula for spring ${{S}_{1}}$
i.e. $P{{E}_{1}}=\dfrac{1}{2}K{{r}^{2}}$ …… (1)
Similarly, we use the above formula for spring ${{S}_{2}}$
i.e.$P{{E}_{2}}=\dfrac{1}{2}2K\text{ }{{x}^{2}}$ …… (2)
Now, dividing equation (2) by equation (1)
We get $\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}K{{x}^{2}}\times \dfrac{2}{\left( 2K \right){{x}^{2}}}$
Now, cancelling all the common factors in the above equation we get
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$
Or for simplicity we can write this as also
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$

Therefore, the ratio of the two potential angles is $2:1$

Note Above discussion of Potential Energy that is stored in the spring can be found out using $\dfrac{1}{2}k{{x}^{2}}$formula in which$k=\text{Spring Constant}$.
In this case, we reciprocate this energy with respect to the other.