Question

Two vertical plane mirrors are inclined at an angle of ${60^0}$ with each other. A ray of light travelling horizontally is reflected first from one mirror and then from the other. The resultant deviation is
A. ${60^0}$
B. ${100^0}$
C. ${180^0}$
D. ${240^0}$

Answer 1

Hint: Start with the information given in the question that is angle between the two mirrors, direction of the ray of light falling on the first mirror and then on the second mirror. Then try to find the angle deviation from the horizontal direction of the light ray falling on both the mirrors. Try to use a figure to find out all the angles.

Complete step by step solution:
Angle between the two mirrors is given in the question.
Therefore, $\angle ABC = {60^0}$ (given in question)


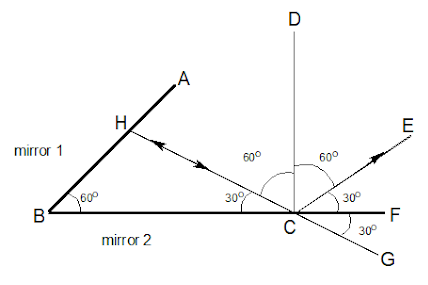
Now from the figure drawn above we can see that a ray of light is falling on the mirror 1 then gets reflected by it and falls on the mirror 2 and then gets reflected in the direction of E. Ray of light is falling horizontally on the mirror 1 therefore,
$\angle BHC = {90^0}$
So, $\angle HBC + \angle BHC + \angle BCH = {180^0}$
Putting the value, we get
${60^0} + {90^0} + \angle BCH = {180^0}$
After solving we get;
$\angle BCH = {30^0}$

If we draw a perpendicular line on C that is DC, we get;
$\angle DCH = {60^0}$
similarly we get;
$\angle DCF = {60^0}$
Therefore $\angle ECF = {30^0}$
From alternate angle we $\angle FCG = {30^0}$
Now we have to find the angle of deviation x
From the figure above we get;
$x = {180^0} + \angle GCF + \angle FCE$
$\Rightarrow x = {180^0} + {30^0} + {30^0}$
$\therefore x = {240^0}$

Hence the correct answer is option D.

Note: Be careful about the direction of the ray of light falling on both the mirrors, here it is horizontal if it is vertical then the answer will also change. Be careful about all the angles. Use the given information from the question to draw the required figure and then put all the value of the angle.