How to Add Like and Unlike Fractions with Formula and Solved Examples
You must know about fractions. Fraction is a part of the whole. In fractions, we have a numerator and denominator; the numerator represents parts, and the denominator represents the whole in the fraction. In this article, you will be learning about the addition of fractions.
In addition of fractions, when the denominators are the same, then the addition of fractions seems easy, but when denominators are different then, how will you add them?
Fractions
Before we get into the matter, we need to know what a fraction is, what a like and unlike fraction is, and how to convert an unlike fraction to a like fraction.
There are numerous ways to make fractions enjoyable for children. As we deal with fractions daily, it's simple to let them enjoyably explore the concept.
Definition of a Fraction
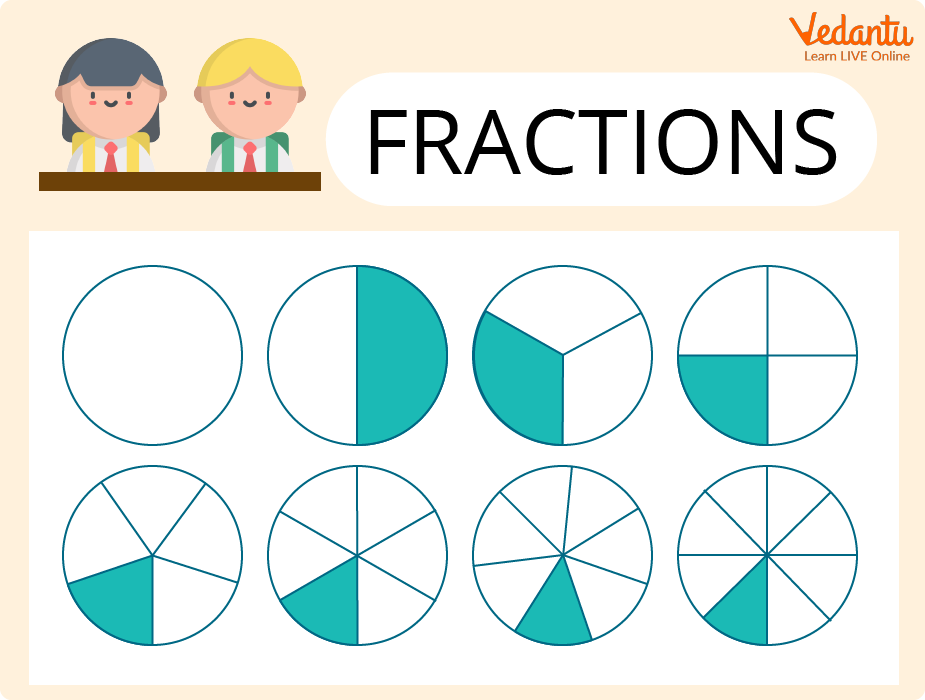
Learning Fractions
Fractions are used to represent smaller portions of a larger whole. The components could make up a single thing or multiple things. In any case, they combine to form what is known as a whole.
Types of Fractions
Adding Fractions
To add fractions successfully, students must first understand the differences between each type of fraction.
Parts of a whole are represented by fractions. In a fraction, the denominator represents the number of equal parts in a whole, and the numerator represents how many parts are being considered.
Circle Divided Into Four Parts
The circle is divided into four parts in the diagram above. As a result, the fraction is $\dfrac{1}{4}$ or a quarter.
Proper, improper, and mixed fractions are the three types of fractions.
Proper Fraction: The numerator is less than the denominator. e.g- $\dfrac{3}{4}$ (three quarters)
Improper Fraction: The numerator is greater than the denominator. e.g- $\dfrac{7}{4}$ (seven quarters)
Mixed Fraction: A whole number and a proper fraction combined. e.g- $1\dfrac{3}{4}$ (one and three quarters).
Furthermore, fraction equations will be divided into two groups:
Like fractions: Fractions with the same denominator. e.g- $\dfrac{1}{4}$ and $\dfrac{3}{4}$
Unlike fractions: Fractions with different denominators. e.g- $\dfrac{1}{4}$ and $\dfrac{3}{8}$
How to Add Two Fractions- Steps for Adding Fractions
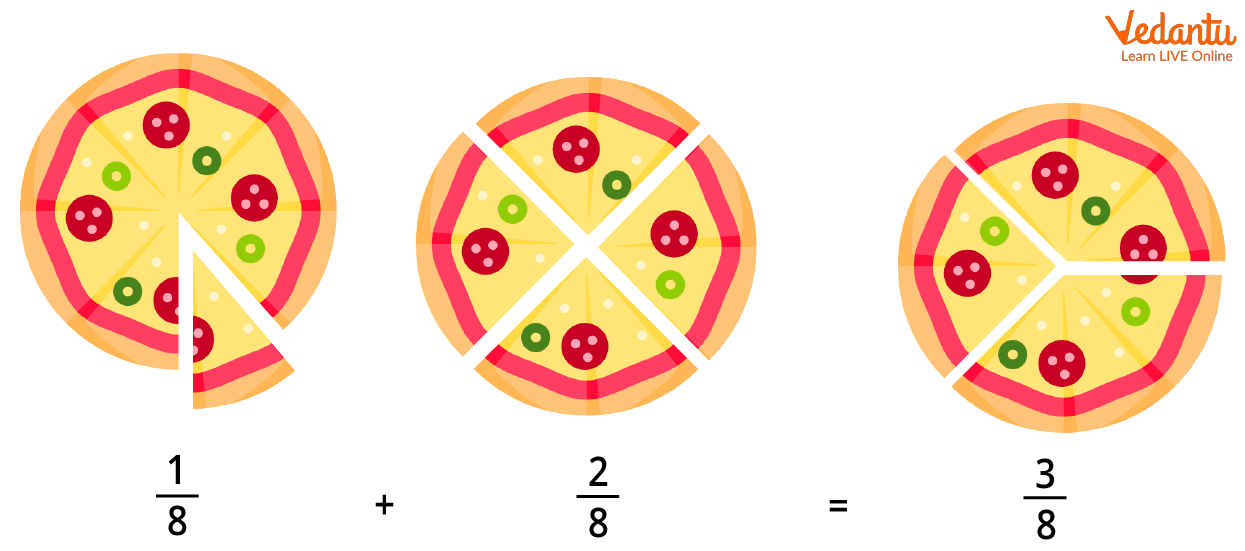
Teaching Addition Through Pizza Slices
The Addition of Fractions may appear difficult at first, but with practice, you'll be up and running as quickly as possible.
Here are a few steps on how to add fractions:
Check to see if the denominators of the fractions are the same.
Convert them to equivalent fractions with the same denominator if they don't have the same denominator.
Add the numbers in the numerator once they have the same denominator.
Put the new numerator over the denominator in your answer.
When you converted the fractions to the same common denominator, the denominator may have changed.
Tips for Adding Fractions
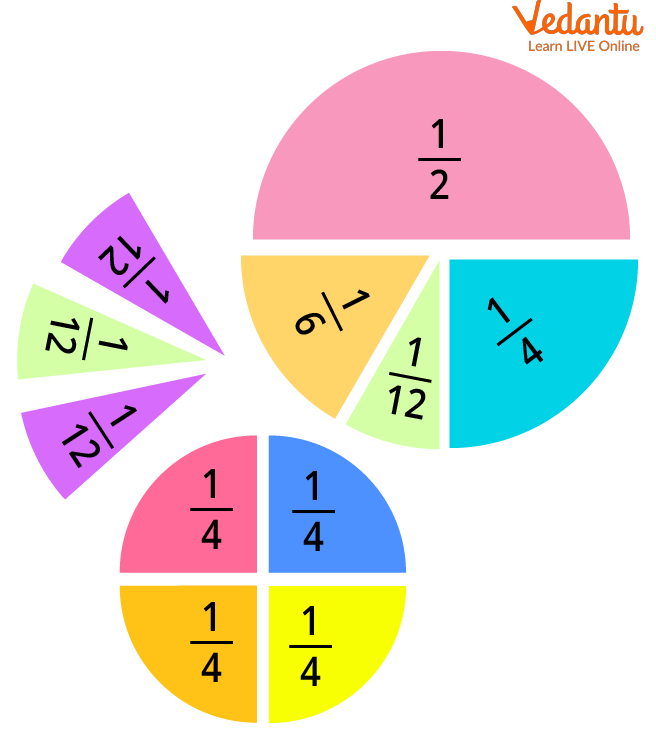
Learning Fractions in Part-whole
Before you add fractions, make sure the denominators are the same.
The value of a fraction remains the same when the top and bottom are multiplied by the same number.
Converting fractions to common denominators should be practised. Adding fractions is the most difficult part.
After you've finished the addition of fractions, you might need to simplify your answer.
If you're adding mixed numbers, make sure to convert them to improper numbers first.
Addition of Fraction Examples
Addition of Fraction With Same and Different Numerator
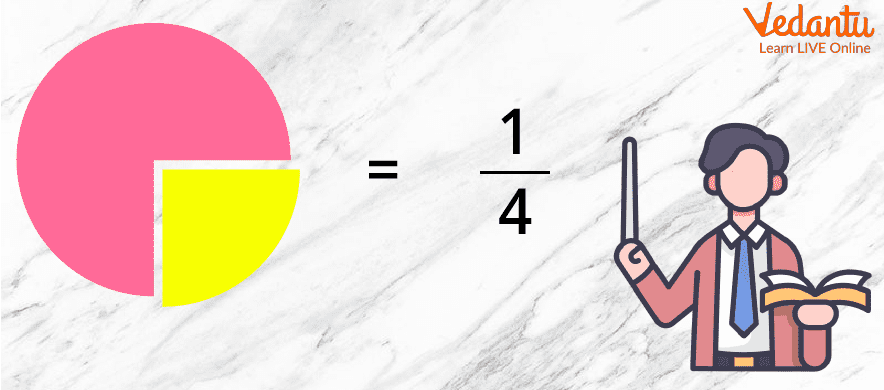
Let’s Learn
Following are examples of the addition of fractions-
Example 1: ($\dfrac{5}{8}+\dfrac{2}{8}$)=?
Step 1: Denominators are the same.
Step 2: Take the numerators 5 and 2, respectively and add them.
= $\dfrac{5+2}{8}$
Step 3: Give the final answer.
= $\dfrac{7}{8}$
In the above example, we learned how to add two fractions.
Example 2: $\dfrac{3}{8}+\dfrac{5}{12}$=?
Step 1: Denominators are different. So, take the Least Common Multiple (LCM).
24 is a common multiple of 8 and 12.
Step 2: Make the denominators equal by multiplying $\dfrac{3}{3}$ with $\dfrac{3}{8}$ and multiplying $\dfrac{2}{2}$ with $\dfrac{5}{12}$.
$\Rightarrow \dfrac{3}{8}=\dfrac{3}{8}\times \dfrac{3}{3}$
$=\dfrac{9}{24}$
Also, $\Rightarrow \dfrac{5}{12}=\dfrac{5}{12}\times \dfrac{2}{2}$
$=\dfrac{10}{24}$
Step 3: Take the numerators and add.
$\Rightarrow \dfrac{3}{8}+\dfrac{5}{12}$
$=\dfrac{9}{24}+\dfrac{10}{24}$
$=\dfrac{9+10}{24}$
Step 4: Answer = $\dfrac{19}{24}$
In the above example, we learned the addition of fractions with different denominators.
Types of Fractions
Let’s Practice
Solving Problems
Learning from the addition of fractions examples, let us solve the following problems on our own. Following are the fraction addition sums-
1. Add: $\dfrac{7}{10}+\dfrac{2}{10}$ (Ans: ($\dfrac{9}{10}$))
2. Add: $\dfrac{5}{10}+\dfrac{2}{10}$ (Ans: ($\dfrac{7}{10}$))
Summary
To summarise, students must understand that fractions are more than just shading and colouring. A fraction is a part of the whole. A common fraction is a numeral which represents a rational number. Fractions are numbers that lie between two consecutive whole numbers. Use fractions in everyday conversations as a parent, relate fractions to real-life situations and provide examples from everyday activities such as cooking, baking, time, and measurement.
FAQs on Addition of Fractions Explained with Methods and Examples
1. What is addition of fractions?
The addition of fractions is the process of combining two or more fractions to find their total value. If the denominators are the same, add the numerators and keep the denominator unchanged. If the denominators are different, first convert them to equivalent fractions with a common denominator, then add the numerators. For example, 2/7 + 3/7 = 5/7.
2. How do you add fractions with the same denominator?
To add fractions with the same denominator, add the numerators and keep the denominator the same.
- Step 1: Add the numerators.
- Step 2: Keep the common denominator.
- Step 3: Simplify if needed.
3. How do you add fractions with different denominators?
To add fractions with different denominators, first find a common denominator, then add the numerators.
- Step 1: Find the LCM of the denominators.
- Step 2: Convert each fraction to an equivalent fraction.
- Step 3: Add the numerators and keep the common denominator.
4. What is the formula for adding fractions?
The formula for adding two fractions is a/b + c/d = (ad + bc) / bd. This formula works when denominators are different. Multiply each numerator by the other fraction’s denominator, add the results, and place over the product of the denominators.
5. How do you find a common denominator when adding fractions?
A common denominator is found by calculating the Least Common Multiple (LCM) of the denominators.
- List multiples of each denominator.
- Choose the smallest common multiple.
- Convert each fraction to an equivalent fraction using that denominator.
6. Can you give an example of adding mixed fractions?
To add mixed fractions, convert them into improper fractions first, then add normally. Example: 1 1/2 + 2 1/3.
- Convert: 1 1/2 = 3/2 and 2 1/3 = 7/3.
- Find LCM of 2 and 3 = 6.
- Convert: 9/6 + 14/6 = 23/6.
- Convert back: 23/6 = 3 5/6.
7. Do you always need to simplify after adding fractions?
Yes, you should simplify the final answer to its lowest terms whenever possible. After adding, divide the numerator and denominator by their greatest common factor (GCF). Example: 6/8 = 3/4 after dividing by 2.
8. What are common mistakes when adding fractions?
A common mistake when adding fractions is adding denominators directly, which is incorrect.
- Wrong: 1/2 + 1/3 = 2/5.
- Correct method: Find LCM (6), then 3/6 + 2/6 = 5/6.
- Forgetting to simplify the final answer.
9. How do you add more than two fractions?
To add more than two fractions, convert all fractions to a common denominator and then add the numerators. Example: 1/4 + 1/6 + 1/3.
- LCM of 4, 6, and 3 is 12.
- Convert: 3/12 + 2/12 + 4/12.
- Add: 9/12 = 3/4.
10. Why do we need a common denominator to add fractions?
We need a common denominator because fractions must represent equal-sized parts before they can be added. The denominator shows the size of each part, so different denominators mean different part sizes. Converting to a common denominator ensures the fractions measure the same type of parts before adding.
