Addition Theorem of Probability Explained with Formula and Applications

Probability defines the likelihood of an event occurring. There are many situations in real life where we may need to predict the outcome of an event. We may or may not be certain of the outcome of the event. In such cases, we say that there is a probability that the event will or will not occur. Probability in general has great applications in games, and in business for making predictions based on probability, and also probability has extensive applications in this new field of artificial intelligence.

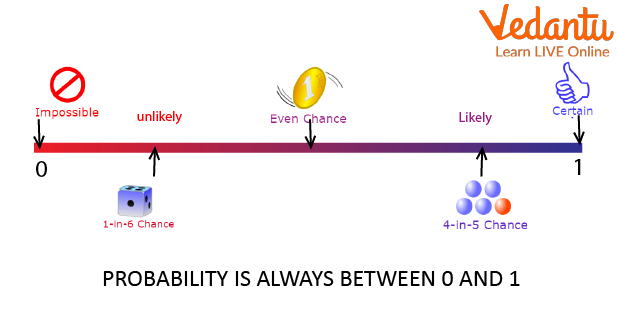
The probability of an event can be calculated using the probability formula simply by dividing the number of favorable outcomes by the total number of possible outcomes. The probability value of an event occurring can lie between 0 and 1, since the number of favourable outcomes can never exceed the total number of outcomes. Also, a favorable number of results cannot be negative. Let's discuss the basics of probability in detail in the following sections.

Theory of Probability

Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event. For an experiment that has "n" number of outcomes, the number of favorable outcomes can be denoted by x. The formula for calculating the probability of an event is as follows.

Probability(Event) = Favorable Outcomes/Total Outcomes = x/n

Probability

Additional Theorem With Example

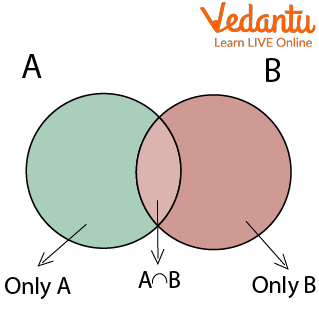
If $A$ and $B$ are any two events of a random experiment and $P$ is a probability function then the probability of happening of at least one of the events is defined as $P(A \cup B)=P(A)+P(B)-P(A \cap B)$.

Now, we have to prove the Addition theorem of probability.

Given: A and B are any two events of a random experiment.

To prove: $P(A \cup B)=P(A)+P(B)-P(A \cap B)$.

Proof:

From the set theory we know that

$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

Suppose $n(S)$ denote the total number of the possible events of random experiment and then dividing both left hand side and right hand side of the of the above equation we get,

$\frac{P(A \cup B)}{n(S)}=\frac{P(A)}{n(S)}+\frac{P(B)}{n(S)}-\frac{P(A \cap B)}{n(S)}$

Now, we know that a formula for probability $P(x)=\frac{n(x)}{n(S)}$. By applying this we can write

$P(A \cup B)=P(A)+P(B)-P(A \cap B)$

Hence, the above given additional theorem of probability is proved.

Additional Theorem Of Probability

Examples:

As per the expansion hypothesis, if two occasions A and B are fundamentally unrelated, the probability of one or the other A or B happening is all out of the singular probabilities of A and B.

For two fundamentally unrelated occasions A, B

P(A or B)=P(A)+P(B)

Example for addition theorem of probability for 3 events: If $A, B$ and $C$ are three events in the sample space $S$. Then,

$P(A \cup B \cup C)=P(A)+P(B)+P(C)-P(A \cap B)-P(B \cap C)-P(C \cap A)+P(A \cap B \cap C)$

If $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three mutually exclusive events, then

$P(A \cup B \cup C)=P(A)+P(B)+P(C)$

Summary

Probability is a branch of mathematics concerned with numerical descriptions of how likely an event is to occur or how likely a statement is to be true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates the impossibility of the event and 1 indicates certainty.