Application of Heron's Formula to Find Areas of Quadrilaterals

Application of Heron's formula to find areas of Quadrilaterals 

In this article, we use Heron’s formula or Heron's formula to find the area of different types of triangles. To use this Heron’s formula, we don’t need to know the angle of the triangle; only the sides of the triangles are enough. Hero of Alexandria derived this formula. He then extended this heron’s formula to find the area of quadrilateral and higher-order polygons. Thus, we can find the area of a quadrilateral by dividing it into two triangles along its diagonal. 

Steps to find Area using Heron’s Formula

The following are the steps used to find the area of the triangle using Heron’s formula:

i. First, find the perimeter of the given triangle.

ii. Next find the semi-perimeter value i.e. \[S = \frac{{a + b + c}}{2}\]

iii. And, then use Heron’s formula to find the area of triangle \[ = \sqrt {s(s - a)(s - b)(s - c)} \]

iv. Lastly add accurate units i.e. \[{m^2},c{m^2}\], etc.

Heron’s Formula for Equilateral Triangle

A triangle with all its sides equal is called an Equilateral Triangle. 

Equilateral Triangle

First, we will find the semi-perimeter of the equilateral triangle, i.e. \[S = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\] where a is the length of the side. Next, as per heron’s formula, we have the area of the triangle as:

Area \[ = \sqrt {s(s - a)(s - b)(s - c)} \] 

As a=b=c

Area\[ = \sqrt {s{{(s - a)}^3}} \] is Heron's formula for an equilateral triangle.

Heron’s Formula for Isosceles Triangle

A triangle with all two sides equal is called the Isosceles Triangle, and the angles corresponding to these two sides are congruent. 

Isosceles (Right angled) Triangle

 

First, we will find the semi perimeter of the isosceles triangle, i.e. \[S = \frac{{a + a + b}}{2} = \frac{{2a + b}}{2}\] where a is the length of the congruent sides and ‘b’ is the length of the base. Next, as per heron’s formula, we have the area of the triangle as:

Area \[ = \sqrt {s(s - a)(s - b)(s - c)} \] 

As it is an isosceles triangles i.e. a = b, c = b

\[ = \sqrt {s(s - a)(s - a)(s - b)} \]

Area\[ = \sqrt {s{{(s - a)}^2}(s - b)} \] or Area \[ = (s - a)\sqrt {s(s - b)} \] is the Heron’s formula for isosceles triangle.

Heron’s Formula for Scalene Triangle

A triangle with all three sides not equal is called the Scalene Triangle. It is also known as the Irregular Triangle. 

Scalene (Irregular) Triangle

First, we will find the semi-perimeter of the scalene triangle i.e. \[S = \frac{{a + b + c}}{2}\] where ‘a’, ‘b’, and ‘c’ are the length of the sides of the triangle. Next, as per heron’s formula, we have the area of the triangle as:

Area \[ = \sqrt {s(s - a)(s - b)(s - c)} \] is Heron’s formula for isosceles triangle.

Heron’s Formula for Quadrilateral

Suppose ABCD is a quadrilateral where \[AB\parallel CD\]and AC and BD are the diagonals. Let’s suppose AC divides into two triangles, i.e. \[\Delta ADC\]and\[\Delta ABC\].

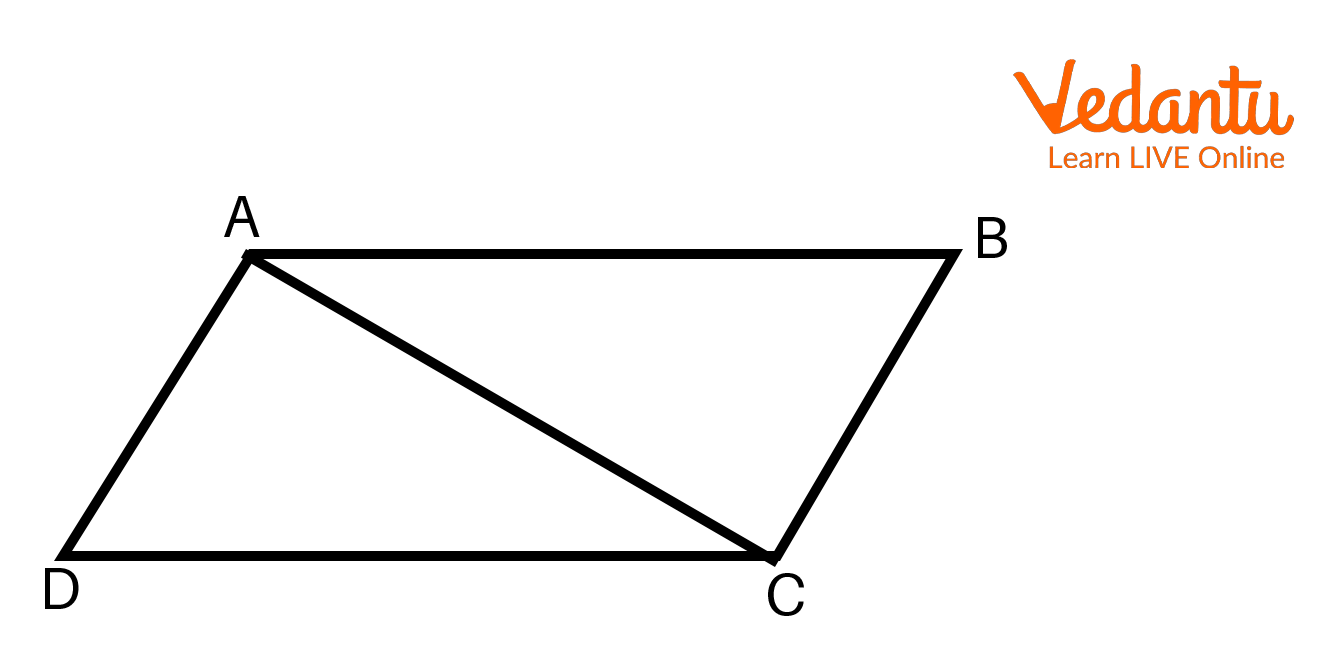
Quadrilateral ABCD

Area of = Area of \[\Delta ADC\] + Area of \[\Delta ABC\].

If we know the length of all the sides of the quadrilateral and the length of AC, we can know using Pythagoras's Theorem. After that, we can find the area of each triangle using Heron’s formulas and add the areas of the triangles to get the area of the quadrilateral using Heron’s formula.

Application of Heron’s Formula 

The main applications of Heron’s formula (when all three sides/lengths are given) are:

1. Find the area of different types of a triangle.

2. Find the area of a quadrilateral.

3. Used in applications in trigonometry such as to provide the law of cosines, the law of cotangents, etc

Interesting Facts

• Area of Right angled triangle \[ = \frac{1}{2} \times base \times height\]

• If a triangle and a parallelogram lie on the same base and between the same set of parallel lines, then the area of the triangle is half of the area of the parallelogram.

Important Questions

1. We are given lengths of all three sides as 25cm, 6cm, and 39cm. Find the area of the triangle.

Solution:

First, we will find the semi-perimeter as:

\[S = \frac{{a + b + c}}{2}\]

\[ \Rightarrow S = \frac{{25 + 56 + 39}}{2}\]

\[ \Rightarrow S = \frac{{120}}{2} = 60\]

Next, the area of the triangle is:

\[ = \sqrt {s(s - a)(s - b)(s - c)} \]

\[ = 420\] sq cm

Hence, the area of the triangle is 420 sq cm.

2. If given the length of the three sides of the triangle as 17cm, 17cm, and 16cm. Find the area of the triangle using two methods.

Solution:

1) By using Pythagoras Theorem (\[\Delta ADB\]):

Find the Area of the Triangle  

\[\therefore A{D^2} = A{B^2} - B{D^2}\]

\[ \Rightarrow A{D^2} = 289 - 64 = 225\]

\[ \Rightarrow AD = 15\] cm

Thus, the area of the isosceles \[\Delta ABC\]

\[ = \frac{1}{2} \times base \times height\]

\[ = \frac{1}{2} \times 16 \times 15\]

\[ = 120\]sq cm

2) Heron’s Formula

First, find the semi-perimeter of a triangle

\[S = \frac{{a + b + c}}{2}\]

\[ \Rightarrow S = \frac{{17 + 17 + 16}}{2}\]

\[ \Rightarrow S = \frac{{50}}{2} = 25\]

Next, the area of the triangle is

\[ = \sqrt {s{{(s - a)}^2}(s - b)} \]

\[ = \sqrt {25{{(25 - 17)}^2}(25 - 16)} \]

\[ = \sqrt {25{{(8)}^2}(9)} \]

\[ = \sqrt {{{(5)}^2}{{(8)}^2}{{(3)}^2}} \]

\[ = 5 \times 8 \times 3 = 120\]sq m

Hence, the area of the triangle is 120sq m.

3. In a parallelogram ABCD diagonal BD = 18 cm, perimeter of the parallelogram = 60 cm and AB = 2BC. Find the area of .

Solution:

According to the given information, we get the following:

Parallelogram ABCD

As we know, opposite sides of the parallelogram are equal

AB = CD and BC = DA                                   ------- (1)

Also, perimeter of = (AB + BC + CD + DA) = 60 cm                  (given)          ------ (2)

\[\therefore AB + BC + AB + BC = 60\]

\[ \Rightarrow 2AB + 2BC = 60\]

\[ \Rightarrow 2(AB + BC) = 60\]

\[ \Rightarrow AB + BC = 30\]cm                                   ------- (3)

Next, 

\[\therefore 2BC + BC = 30\]

\[ \Rightarrow 3BC = 30\]

\[ \Rightarrow BC = 10\]cm                                             -------- (4)

And, given that \[AC = 2BC\] 

\[ \Rightarrow AB = 2 \times 10 = 20\] cm

Now  from (1), we have

AB = CD = 20cm                                ------- (5)

BC = DA = 10cm                                ------- (6) 

Also, we know that the diagonal of a parallelogram divides it into two congruent triangles

\[ \Rightarrow \Delta ABD \cong \Delta CDB\]

\[ \Rightarrow \] Area of \[\Delta ABD\]= Area of \[\Delta CBD\]

\[ \Rightarrow \]Area of = 2 (\[\Delta ABD\])                  ------- (7)

Next, the Heron’s Formula is

\[ = \sqrt {s(s - a)(s - b)(s - c)} \] where a=20cm, b=18cm, c=10cm

So, the semi-perimeter is:

\[s = \frac{{a + b + c}}{2}\]

\[ \Rightarrow s = \frac{{AB + BD + DA}}{2}\]

\[ \Rightarrow s = \frac{{20 + 18 + 10}}{2} = 24\]cm

Thus, area of the \[\Delta ABD\] using the Heron’s Formula is:

\[ = \sqrt {s(s - a)(s - b)(s - c)} \]

\[ = \sqrt {24(24 - 20)(24 - 18)(24 - 10)} \]

\[ = \sqrt {24(4)(6)(14)} \]

\[ = 24\sqrt {14} \]sq cm

Now from (7), we have

\[\therefore \]Area of = 2 (\[\Delta ABD\])

\[ \Rightarrow \]Area of \[ = 2 \times 24\sqrt {14} \]\[ = 48\sqrt {14} \]sq cm 

Hence, the area of parallelogram ABCD is \[48\sqrt {14} c{m^2}\]

Conclusion

The article summarizes the theorem of equal chords and their distances from the center i.e. equal chords are equidistant from the center and then converse too. Then we learned the theorem of the intersection of equal chords too. Also, this article has solved examples to understand the concepts easily.

Practice Questions

1. If the lengths of the sides are 12m, 11m, and 5m. Find the area of the triangle.

2. Can we find the area of these polygons?

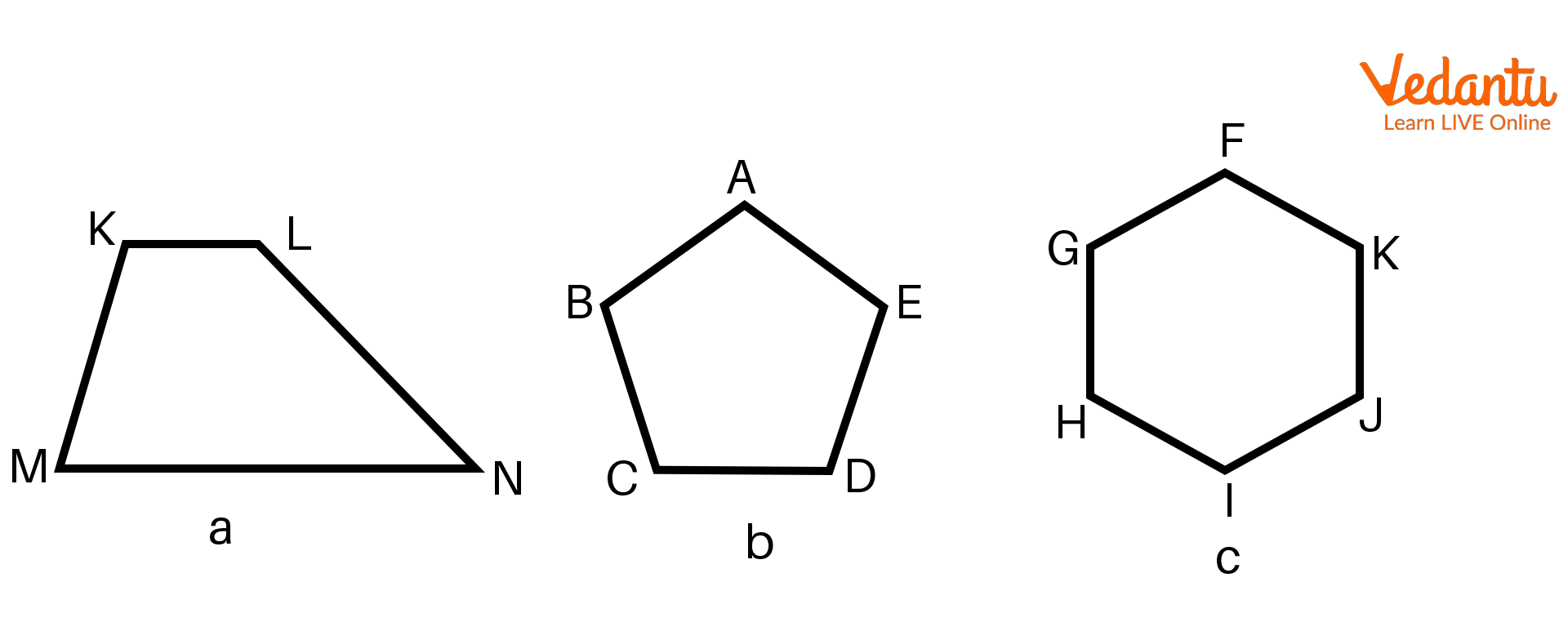
Different Types of Polygons

1. Yes

2. No

3. Can’t determined

Answers:

1) 27.5 sq m

2) A

List of Related Articles

• Derivation of Heron Formula

• Types of Triangles

• Area of Quadrilateral