What is the Circumference of a Circle?
When you see a ball, the outer periphery of the ball which is visible to you is the circumference of the ball. So in simple terms, Circumference is nothing but the perimeter of a circle or an elliptical object. The concept is not only fun in learning rather it is fun in teaching also. In this article, we bring you a very important and interesting concept of geometry which is the Circumference of a circle.
Circumference of a Circle - Definition
The circumference of a circle is the length of the boundary of the circle. If we cut open the circle and straighten it the length of the boundary will be the measure of the circumference of the circle.
A circle is made up of many points arranged equidistant from a single central point and The point is known as the centre of the circle.
The distance between the centre and any point on the circumference is known as the radius of the circle. The radius is a constant value. It doesn’t change.
The diameter of a circle is the maximum distance between any two points on the circumference. It is twice the radius.
The Formula for Circumference of the Circle
The circumference of a circle is measured in units of length like meter, centimetre, etc. The formula for calculation of circumference is,
Circumference = 2πR
Where R is the radius of the circle,
π (pi) is a constant value.
The value of π = 3.1415926535897…
π or pi is a Greek letter. It is a very important constant in mathematics. It gives the ratio of circumference to the diameter of a circle or the ratio of circumference to twice the radius. For any given circle, this ratio will remain π. It is a constant so whatever be the circumference and the radius the ratio will be equal to π. π is an irrational number hence it cannot be written down as a finite decimal number. Its value is 3.1415926535… Its value goes on to infinite decimal places.
But using an infinite number will make calculations almost impossible. Therefore, for calculations, we can use π = 22/7. This makes calculations easier. We can also take the value of π = 3.14. For even more simplification one can take the value of π = 3.
Question: Find the circumference of a circle if the radius is 14 cm. (use π = 22/7)
Answer: R(given) = 14 cm
Circumference = 2πR
= 2 * 22/7 * 14
= 88 cm
Questions:
1. If the circumference of a circle is 24 cm, find the radius of this circle.
2. Find the circumference of a circle if the radius is 22 cm. (use π = 22/7).
3. Find the circumference of a circle if the radius is 36 cm. (use π = 3.14).
4. If the circumference of a circle is 120 cm, find the radius of this circle.
5. If the circumference of a circle is 68 cm, find the radius of this circle.
Basic Components of Circle
1. Centre of the circle:
The center of a circle is the center point in a circle from which all the distances to the point on the circle are equal.
2. Diameter:
A chord or a line passing through the center of a circle is called the diameter. The diameter is considered to be the longest chord in the circle. The diameter is twice the radius.
3. Radius:
The constant distance from its centre is called the radius of the circle.
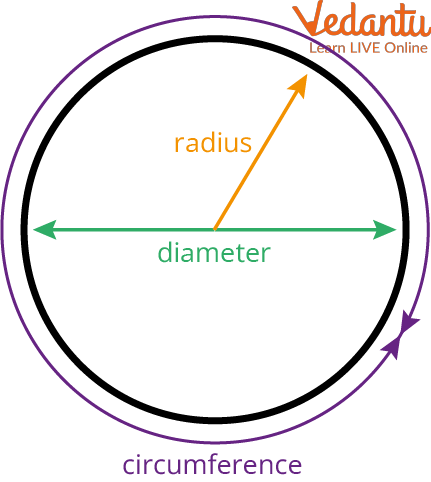
The Components of the Circle
Area of a Circle
The area of a circle is the area bounded by the circumference.it is the area inside the circumference. The circumference is the only length. Its width is zero. It is one-dimensional.
The area is not one-dimensional. The formula for calculation of the area of a circle is given by,
Area= πR2
Where R is the radius of the circle,
π is constant.
Here again, the value of π is non-terminating. Therefore, for easier calculations, we can use π = 3.14 or π = 22/7.
If we need to calculate the circumference of a circle whose area is given, we will first find the radius from the area and then put it in the formula for circumference.
From the area to get the radius, we should first divide by π and then find the square root of it. This will give us the radius. Next simply, put the value of the radius in the formula for circumference to find the circumference.
One can also find the area of a circle if the circumference is given. For this first, we have to divide the circumference by π and then by 2. This will give us the radius. Then put the radius in the area formula to calculate the area.
Properties of Circle
A circle consists of some properties
i) The outer line of the circle is equidistant from the center.
ii) The diameter of the circle divides it into 2 equal parts and passes through the center.
iii) Circles which are different in size or have different radii are similar.
iv) The diameter of the circle is the largest chord and is doubled the radius.
Solved Example of Circumference of the Circle
Q 1. What is the circumference of a circle with a radius of 7 cm?
Ans: Circumference or $\mathrm{C}=2 \pi \mathrm{r}=2 \times \pi \times \mathrm{r}=2 \times \dfrac{22}{7} \times 7=44 \mathrm{~cm}$
Q 2. What is the circumference of the circle whose diameter is 6cm?
Ans: $C=\pi \times d=\dfrac{22}{7} \times 6=18.8 \mathrm{~cm}$
Area of The Circle
The area of the circle is the space captured by the circle in the plane. The space occupied within the boundary circumference of the circle is called the area of the circle.
The formula for the area of the circle is,
$A=\pi r^{2} \text { or }$
$A=\dfrac{\pi}{4} \times d^{2}$
It is useful for measuring the region occupied by the circular field
Area of the Circle
Solved Example of an Area of the Circle
Q 1. If the length of the radius of a circle is 4 units. Calculate its area.
Ans: Radius $(r)=4$ units
Area of the circle $=\pi r^{2}$
$A=\dfrac{22}{7} \times 4^{2}=50.27 \mathrm{sq} .$ Units
Q 2. The length of the largest chord of a circle is 12 units. Find the area of the circle.
Ans: The largest chord of the circle is the Diameter $(\mathrm{d})=12$ units
Area of the circle $=\dfrac{\pi}{4} \times d^{2}=\dfrac{22}{7} \times 12 \times 12=113.1$ square units.
Practice Questions
Q 1. Use the relevant formula to calculate the circumference of the circle whose radius is 6 cm.
Ans: 37.71 cm
Q 2. Calculate the area of the circle given the radius of $6 \mathrm{~cm}$.
Ans: $113.14 \mathrm{~cm}^{2}$
Q 3. Calculate the area of the circle whose diameter is $10 \mathrm{~cm}$.
Ans: $314.28 \mathrm{~cm}^{2}$
Q 4. Calculate the area circle id radius $8 \mathrm{~m}$ in terms of $\pi$.
Ans: 64 $\pi \mathrm{m}^{2}$
Conclusion
This is how we calculate the circumference of a circle and understand its difference from the area. It is a one-dimensional physical quantity that can be easily understood and calculated if we follow how the formula is determined. Focus on the solved examples and start using the formula to understand the concept better.
FAQs on Circumference of a Circle
1. What are the other circumferences formulas apart from the formula of the circumference of a circle?
Go through the following list to know the other formula of a circumference -
Circumference of a semicircle = C = (πr + 2r)
Circumference of a triangle = a + b + c i.e adding the length of all the sides of a triangle
Circumference of a sphere = C = 2πr.
Circumference of a quadrant C = (π2 + 2)r.
2. What is the circumference of the earth?
If you know the radius of the Earth you can easily find out its circumference by using the formula of the circumference of a sphere as Earth is a spherical object. The formula for which is 2πr and the radius of the Earth is 6378.1 km.
Therefore, applying the formula you would get the circumference as 40,0075 km.
Try finding out the circumference of other spherical objects by knowing the radius of the object and applying the formula.
3. Can you prove that the circumference of a circle is 2πr?
The mathematical formulas usually come with a set of theorems and proves. The scientific nature of the subject makes it possible to prove any of the established formulas or theories. Similarly, the formula of the circumference of a circle has been proven. Follow the link where the subject experts have explained in detail and proved that the circumference of a circle is 2πr.
