Comparing Fractions

By comparing fractions, we mean determining which is the larger and which is the smaller fraction. Numerators and denominators of fractions are compared using a set of rules because they are composed of two parts. Let us learn more about comparing fractions on this page. The numerator is the number on the upper part of the fractional bar that tells how many pieces of the whole we're talking about. The denominator is located below the fractional bar that tells how many total pieces make up one whole. How do you compare fractions? In this article, we discuss the different methods of how to compare fractions to understand the concept better.

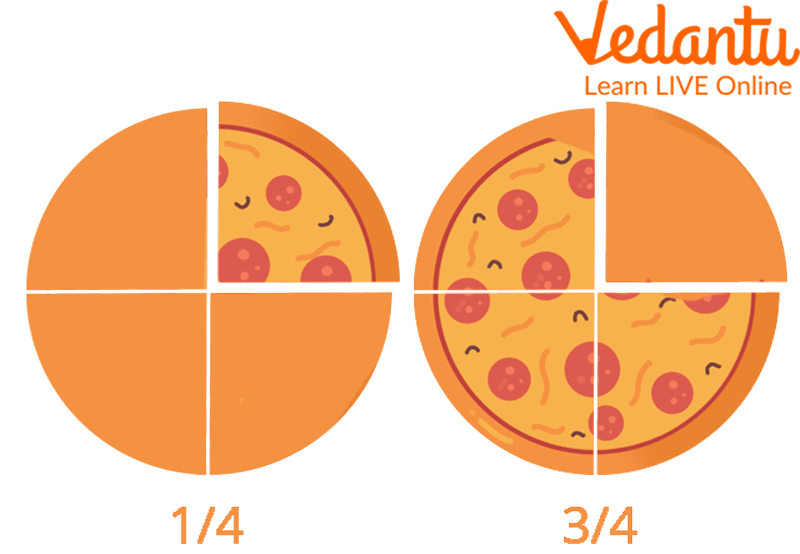
Fractions

Fractions

A fraction can be expressed in the form $\dfrac{a}{b}$, where a, and b are whole numbers and b≠0, in which ‘a‘ is the numerator and ‘b’ is the denominator.

The numbers like $\dfrac{3}{5}$, $\dfrac{2}{3}$, etc., are fractions.

Like and unlike fractions are the two groups of fractions:

• Like Fractions - Fractions with the same denominator.

Example: $\dfrac{1}{7}$, $\dfrac{2}{7}$, $\dfrac{3}{7}$

The denominator of each fraction is the same i.e., 7.

• Unlike Fractions - Fractions with different denominators.

Example: $\dfrac{1}{4}$, $\dfrac{5}{6}$, $\dfrac{1}{3}$

The denominator of each fraction is different.

Comparing Fractions

Finding the greater and smaller fraction between any two or more fractions is known as comparing fractions. Fractions are compared according to a set of rules. In this article, we study more about comparing fractions and comparing unlike fractions and their steps to compare fractions.

Ways of Comparing Fractions

A set of rules relating to the numerator and denominator must be followed while comparing fractions. We can find the greater and smaller fractions by comparing any two fractions. We compare fractions by comparing like fractions and comparing unlike fractions.

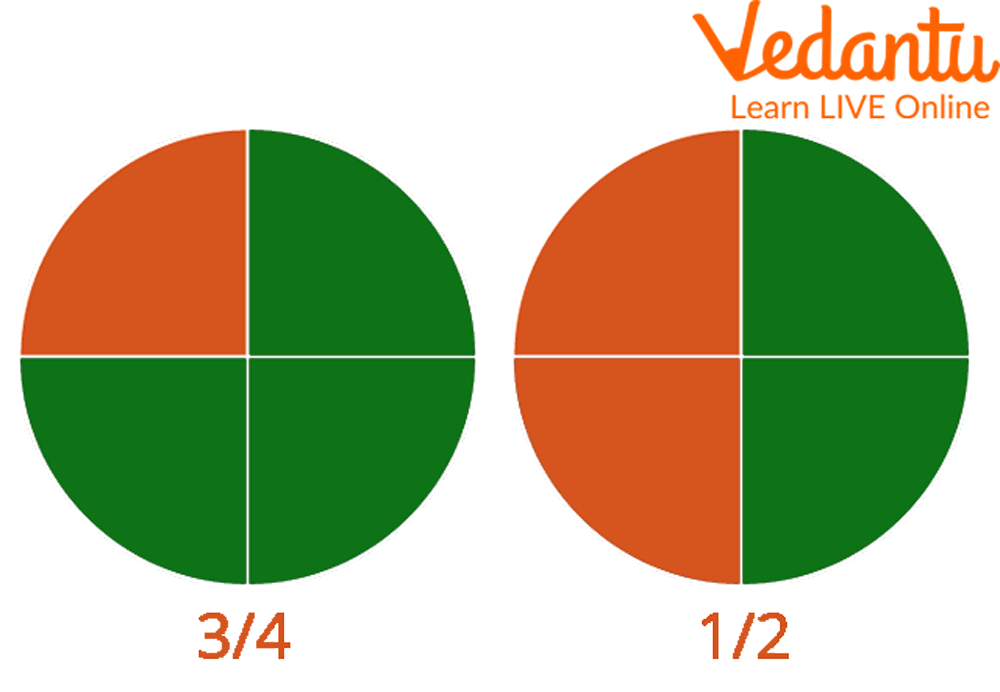
Comparing Fractions

Methods of Comparing Fractions

• Decimal Method

• Same Denominator Method

Comparing Fractions with Unlike Denominators

For comparing fractions with unlike denominators, we must convert fractions from different denominators to similar denominators. For this, we must find the Least Common Multiple(LCM) for the denominators. Then we easily compare the fractions.

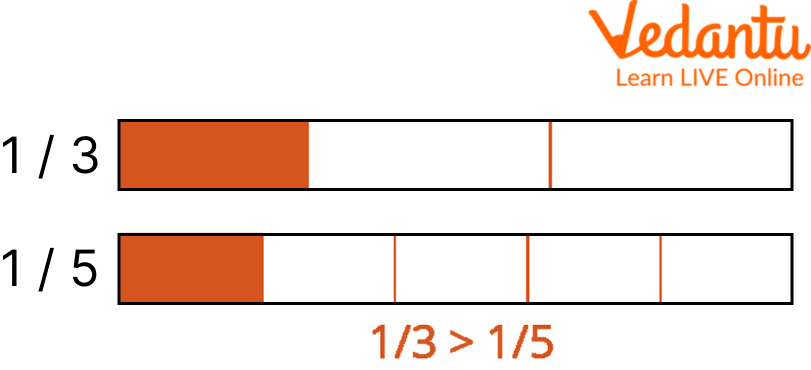
Comparing Unlike Fractions

Method 1: Decimal Method of Comparing Fractions with Different Denominators

This method compares fractional decimal numbers. For this, the fraction is reduced to a decimal form by dividing the numerator by the denominator. The decimal values are then compared. Let's compare $\dfrac{2}{5}$ and $\dfrac{5}{8}$ as an example. These are the following steps to compare fractions:

• Step 1: Write the numbers $\dfrac{2}{5}$ and $\dfrac{5}{8}$ in decimals.

$\dfrac{2}{5}$ = 0.4

$\dfrac{5}{8}$ = 0.625

• Step 2: Evaluate the decimal values. 0.625 > 0.4

• Step 3: The fraction that has a higher decimal value is greater. Hence, $\dfrac{5}{8}$ > $\dfrac{2}{5}$.

Method 2: Same Denominator Method of Comparing Fractions with Unlike Denominators

For comparing fractions with unlike denominators, the Least Common Multiple (LCM) of the denominators should be determined in order to convert them to like denominators. For example, compare $\dfrac{3}{4}$ and $\dfrac{2}{5}$. These are the following steps of the same denominator method:

• Step 1: Check the fractions' denominators, 4 and 5. They are different.

Thus, LCM(4 and 5) = 20.

• Step 2: Now convert their denominators to the same. Multiply the first fraction by $\dfrac{5}{5}$, and the second fraction by $\dfrac{4}{4}$,

i.e., $\dfrac{3}{4} \times \dfrac{5}{5}$ = $\dfrac{15}{20}$

$\dfrac{2}{5} \times \dfrac{4}{4}$ = $\dfrac{8}{20}$

• Step 3: Compare the fractions $\dfrac{15}{20}$ and $\dfrac{8}{20}$. We will compare the numerators because the denominators are the same, so 15 > 8.

• Step 4: The greater fraction is the fraction with the larger numerator, $\dfrac{15}{20}$ > $\dfrac{8}{20}$

So, $\dfrac{3}{4}$ > $\dfrac{2}{5}$.

We can simply compare fractions by looking at their denominators if the denominators are different and the numerators are the same. Fractions with a greater denominator have a lesser value, while fractions with a smaller denominator have a greater value. For example, $\dfrac{2}{3} > \dfrac{2}{6}$

Solved Examples

Q1. Which is larger, $\dfrac{7}{12}$ or $\dfrac{4}{15}$ ?

Ans: The LCM of the denominators 12 and 15.

$\operatorname{LCM}(12, 15)=2 \times 2 \times 3 \times 5=60$

Now, convert the fractions to equivalent fractions with a denominator of 60.

$\dfrac{7}{12}=\dfrac{(7 \times 5)}{(12 \times 5)}=\dfrac{35}{60}$

$\dfrac{4}{15}=\dfrac{(4 \times 4)}{(15 \times 4)}=\dfrac{16}{60}$

Now, observe the numerator, $35>16$.

So, $\dfrac{35}{60}$>$\dfrac{16}{60}$

Therefore, $\dfrac{7}{12}$>$\dfrac{4}{15}$.

Q2. Compare $\dfrac{9}{10}$ and $\dfrac{9}{6}$ with the decimal method.

Ans: First write the fractions in decimals form.

$\dfrac{9}{10}$ = 0.9

$\dfrac{9}{6}$ = 1.5

The fraction that has a higher decimal value is greater. hence, $\dfrac{9}{6}$ > $\dfrac{9}{10}$.

Q3. Shalu has $\dfrac{3}{5}$ of her homework complete and Malini has $\dfrac{3}{4}$ of her homework complete. Who has done more homework?

Ans: The LCM of the denominators 5 and 4 is 20.

Now, convert fractions to equivalent fractions with a denominator of 20.

$\dfrac{3}{5} = \dfrac{(3 \times 4)}{(5 \times 4)} = \dfrac{12}{20}$

$\dfrac{3}{4} = \dfrac{(3 \times 5)}{(4 \times 5)} = \dfrac{15}{20}$

So, $\dfrac{15}{20}$ > $\dfrac{12}{20}$

Therefore, $\dfrac{3}{4}$ > $\dfrac{3}{5}$.

Practice Questions

Q1. Compare $\dfrac{3}{8}$ and $\dfrac{8}{9}$ which is greater?

Ans: $\dfrac{8}{9}$

Q2. Arrange the fractions $\dfrac{5}{4}$, $\dfrac{7}{4}$, $\dfrac{2}{9}$, and $\dfrac{5}{8}$ in Ascending order.

Ans: $\dfrac{2}{9}$, $\dfrac{5}{8}$, $\dfrac{5}{4}$, $\dfrac{7}{4}$

Q3. Rajni ate $\dfrac{9}{22}$ part of the pizza and Irfan ate $\dfrac{5}{11}$ part of the pizza. Who ate the greater part of the pizza?

Ans: Irfan ate the greater part of the pizza.

Q4. Jasmine covered a distance of $\dfrac{9}{11}$ km and Madhav covered a distance of $\dfrac{5}{7}$ km. Who covered the greater distance?

Ans: Madhav covered the greater distance.

Summary

In this article, we got to know about comparing fractions. Here we specifically learned about comparing unlike fractions with two different methods, the decimal method, and the same denominator method. You can compare two fractions with unlike denominators by comparing their denominators’ LCM. By comparing fractions, we identify which part is larger and which part is smaller. So, comparing fractions is a very important and regular part of our life.