




How Does a Growing Principal Affect Compound Interest Calculations?
Do you have any knowledge about compound interest? If not, then do not worry, as this article is based on compound interest. Interest can be calculated using two different methods. Simple interest (SI) and compound interest (CI). Simple interest is the cost of a loan or investment. Compound interest is an interest accumulated on the principal and interest together over a given time period. The interest accumulated on a principal over a period of time is also accounted under the principal. Further, the interest calculation for the next time period is on the accumulated principal value. We will discuss compound interest in more detail in this article. We will also go through some solved examples of compound interest with growing principal and talk about the alternative ways to use the formula of compound interest depending on the time.
What is Compound Interest?
Compound interest is the interest that is calculated on both the principal and former interest. As a result, interest on principal and interest from the previous period are included in the total interest for the succeeding period. It is also called the "interest on interest." It is widely used in all financial and commercial transactions.
Here is an illustration of how it increases yearly. You can see the power of compounding:
1st Year: Interest is earned on the principal amount.
2nd Year: Interest is earned on the principal amount plus Interest from the 1st year.
3rd Year: Interest is earned on the principal amount plus Interest from the 1st and the 2nd year.
4th Year: Interest is earned on the principal amount plus Interest from the 1st, 2nd and third year.
Compound Interest Formula
Following the computation of the total amount over some time using the initial principal and the interest rate, the compound interest is calculated. The formula for calculating the amount is given below:
$\mathrm{C.I}=\mathrm{P}\left(1+\dfrac{r}{\mathrm{n}}\right)^{\mathrm{nt}}-\mathrm{P}$
Where P represents the principal amount
n is the frequency or the number of times the interest is compounded annually
r is the interest rate
t is the time
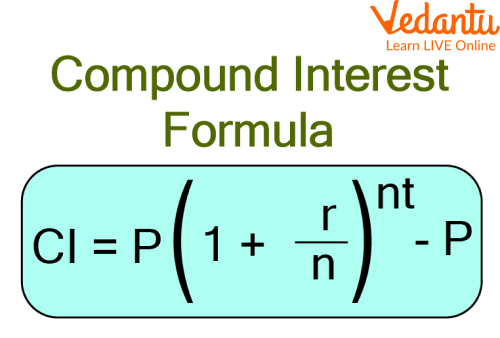
Compound Interest Formula
The Principal amount, as well as the total interest from earlier periods, are used to calculate compound interest.
Compound Interest (CI) =Amount - Principal
$\mathrm{C.I}=\mathrm{P}\left(1+\dfrac{R}{\mathrm{n}}\right)^{\mathrm{nt}}-\mathrm{P}$

Compound Interest Formula
Depending on the problem, compound interest can be calculated daily, weekly, monthly, quarterly, annually etc.
Compound Interest Formulas Table for Different Time Periods
We have provided the formula for compound interest with the growing principal for different periods given below:
Some important points to be kept in mind while learning the principal formula in compound interest:
The principal changes every year when the interest is compounded annually.
In contrast with the original principal, compound interest is based on the amount generated at the end of the previous tenure.
While calculating the compound interest, the rate of interest, and each time period must be of the same duration.
Solved Examples of Compound Interest with Growing Principal
Q1. Find the compound interest on Rs. 8000 for 3 years, compounded annually at $10 \%$ per annum.
Ans: Here, $\mathrm{P}=$ Rs. $8000, \mathrm{R}=10 \%$ per annum and $\mathrm{t}=3$ years
Using the formula, $A=P\left(1+\dfrac{R}{100}\right)^t$
Amount after 3 years $=8000 \times\left(1+\dfrac{10}{100}\right)^3$
$=8000 \times \dfrac{11}{10} \times \dfrac{11}{10} \times \dfrac{11}{10}$
$=10648$
Thus, amount after 3 years $=$ Rs. 1648 .
And compound interest $=$ Rs. $(10648-8000)=2648$.
Q2. Calculate the amount and the compound interest on:
Rs. 8,000 for $1 \dfrac{1}{2}$ years at $10 \%$ per annum compounded yearly.
Ans: Amount $\mathrm{A}=\mathrm{P}(1+\mathrm{r})^{\mathrm{t}}$
Here, $\mathrm{P}=8000, \mathrm{r}=\dfrac{10}{100}=0.1, \mathrm{t}=1 \dfrac{1}{2}=\dfrac{3}{2}=1.5$
$\therefore A =8000(1+0.1)^{1.5}$
$=8000(1.1)^{1.5}$
$=8000(1.1537)$
$=9230$
Compound interest $=9230-8000=1230$
Practice Problems
Q1. Calculate the compound interest on the principal of Rs 5,000 over a year at the rate of 8% per year and compounded half-yearly.
Ans. Rs 408.
Q2. Determine the compound interest for the second and third years on a Rs 20,000 investment made over four years at a 10% annual rate.
Ans. Rs 2200 and Rs 2400.
Summary
Let us recall, compound interest is the interest that is calculated on interest. It is based on both the principal and the interest from the previous period. In this article, we go over compound interest in detail, the formula for calculating compound interest with the growing principal as well as the principal formula in compound interest along with some solved examples. We have provided some questions along with their answers, here in case you want to do some practice on your own.
FAQs on Compound Interest With Growing Principal: Concepts & Formulas
1. What are the differences between Simple Interest and Compound Interest?
Simple interest is based on the principal amount, whereas compound interest is based on the principal amount and the interest compounded throughout the time period. This is the main distinction between simple interest and compound interest. In comparison to compound interest, simple interest offers much lower returns.
2. How much more does compound interest cost than simple interest?
Compound interest can exceed simple interest. For succeeding periods, the value of compound interest changes, we can say that it rises. Simple interest at a rate of 10% would result from an initial principal investment of $100 over a series of 1-year periods but would provide compound interest of $10, $11, $12.1, and $13.31 instead. As a result, compound interest exceeds simple interest.
3. Can the compound interest exceed the principal?
Yes, the compound interest may exceed the principal. For subsequent periods, the value of compound interest changes and rises. The principal of $100 started investing at the rate of 10% over 1 year, which would yield $10, $11, $12.1, and $13.31. Consequently, compound interest grows over time and has the potential to exceed the initial principal value.























