




Step-by-Step Guide: Converting Improper to Mixed Fractions
In Mathematics, fraction is used to show or represent a part of the entire thing. It can represent things as equal parts of the whole. In the representation of fractions, there are two parts namely numerator and denominator.
The number written on the top is known as the numerator. The number written on the bottom part is known as the denominator. The number of equal parts of a thing written on top is called the numerator. The denominator is the whole number in a fraction.
If $\dfrac{5}{10}$ is a fraction.
The number $5$ is a numerator, and $10$ is a denominator.
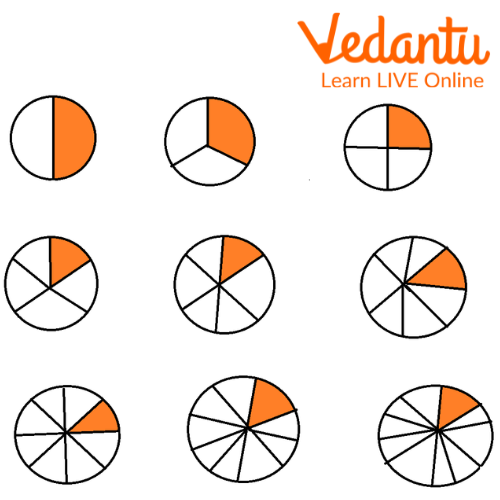
Visual Representation of a Fraction
Improper Fraction
The fractions in which the numerator value is larger than the denominator are known as improper fractions.
E.g. $\dfrac{7}{3}, \dfrac{9}{5}, \dfrac{7}{2}$
Mixed Fraction
It can be defined as the fraction made up of a combination of whole numbers and fractions.
e.g. $3 \dfrac{1}{2}, 5 \dfrac{1}{2}$
How to Convert an Improper Fraction into a Mixed Fraction?
There are certain steps to convert an improper fraction into a mixed fraction. These are discussed below.
First Step: We need to identify the improper fraction.
Second Step: Then, we need to divide the numerator by the denominator and thereby obtain the quotient and remainder.
Third Step: Now, the mixed fraction can be written as:
Quotient (Remainder/Denominator).
Simple Way to Convert Improper Fraction to Mixed Fraction
To convert an improper fraction to a mixed fraction, divide the numerator (upper portion) by the denominator in order to write an improper fraction as a mixed fraction (bottom part). The numerator is the remainder, and the quotient is the entire number.
Solved Examples
Example 1. Let us convert $\dfrac{7}{5}$ into a mixed fraction.
Ans: If in a fraction the numerator and denominator have the same number, it will make a whole.
In the case of $\dfrac{7}{5}, \dfrac{5}{5}$ can be extracted and that can be made a whole.
Therefore, the remaining fraction is $2 / 5$.
So, now we can write $\dfrac{7}{5}$ as the mixed fraction, and that is $1 \dfrac{2}{5}$
The fraction $\dfrac{7}{5}$ means that $7 \div 5$. Now we divide $7$ by $5$ and get $1$ as the quotient making $2$ as the remainder.
In order to convert an improper fraction into a mixed fraction, we need to use the quotient $1$ as the whole number and the remainder $2$ as the numerator whereas the divisor $5$ is used as the denominator of the proper fraction.
Mixed and Improper Fraction.
Example 2. Convert the improper fractions into mixed fractions:
(i) $\dfrac{17}{4}$
Ans: According to the question, the numerator is $17$, and the denominator is $4$
In order to convert the improper fraction into a mixed fraction, we divide the numerator with the denominator.
When we divide $17$ by $4$
Quotient = $4$, Remainder = $1$, Denominator = $4$.
Hence, $\dfrac{17}{4}=4 \dfrac{1}{4}$
(ii) $\dfrac{13}{5}$
Ans: According to the question, the numerator is $13$, and the denominator is $5$
In order to convert the improper fraction into a mixed fraction.
We divide the numerator with the denominator.
When we divide $13$ by $5$
Quotient = $2$, Remainder = $3$, Denominator = $5$.
Hence, $\dfrac{13}{5}=2 \dfrac{3}{5}$
(iii) $\dfrac{28}{5}$
Ans: According to the question, the numerator is $28$, and the denominator is $5$
In order to convert the improper fraction into a mixed fraction.
We divide the numerator with the denominator.
When we divide $28$ by $5$
Therefore, Quotient = $5$, Remainder = $3$, Denominator = $5$
Hence, $\dfrac{28}{5}=5 \dfrac{3}{5}$
(iv) $\dfrac{28}{9}$
Ans: According to the question, the numerator is $28$ and the denominator is $9$
In order to convert the improper fraction into a mixed fraction.
We divide the numerator with the denominator.
When we divide $28$ by $9$
The Quotient = $3$, Remainder = $1$, Denominator = $9$.
Hence, $\dfrac{28}{9}=3 \dfrac{1}{9}$
Practice Questions
Convert the following improper fractions into mixed fractions.
Q 1. Convert into mixed fractions:
(a) $\dfrac{7}{3}$
(b) $\dfrac{11}{7}$
(c) $\dfrac{13}{6}$
Ans: (a) $2^\dfrac{1}{3}$
(b) $\dfrac{14}{7}$
(c) $2^\dfrac{1}{6}$
Q 2. Write improper fraction of $\dfrac{3}{9}$
Ans: $\dfrac{1}{3}$
Summary
Fractions are representations of a single part out of many parts, and they can be in different forms either mixed or improper. Fractions can be converted into either form following a few steps. The steps include identifying an improper fraction, dividing the numerator by the denominator to get a quotient and remainder, and finally, the mixed fraction is written as Quotient (Remainder/Denominator).
Fractions are very useful in expressing a lot of things such as time, i.e. every minute is a part of an hour and every hour is a part of a day.
FAQs on How to Convert Improper Fractions Into Mixed Fractions
1. What is the difference between an improper fraction and a mixed fraction?
An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number), such as 11/4. It represents a value of one or more. A mixed fraction, also called a mixed number, combines a whole number with a proper fraction, like 2 ¾. Both 11/4 and 2 ¾ represent the same value, just in different formats.
2. What are the main steps to convert an improper fraction into a mixed fraction?
To convert an improper fraction into a mixed fraction, follow these key steps as per the CBSE/NCERT 2025-26 curriculum:
Divide the numerator by the denominator.
The quotient (the whole number part of the result) becomes the whole number of the mixed fraction.
The remainder of the division becomes the new numerator of the fractional part.
The denominator remains the same.
3. Can you provide a step-by-step example of converting the improper fraction 35/8 into a mixed fraction?
Certainly. To convert the improper fraction 35/8 into a mixed fraction, you would:
Step 1: Divide the numerator 35 by the denominator 8. When you do 35 ÷ 8, the result is 4 with a remainder.
Step 2: The quotient is 4, which becomes the whole number. The remainder is 3 (since 8 x 4 = 32, and 35 - 32 = 3).
Step 3: Assemble the mixed fraction. The whole number is 4, the remainder (new numerator) is 3, and the denominator stays 8. So, 35/8 becomes 4 ⅜.
4. Why is it useful to convert an improper fraction into a mixed fraction?
The primary reason to convert an improper fraction into a mixed fraction is for better understanding and real-world context. It is much easier for our brains to visualize "2 and a half cakes" (2 ½) than "five-halves of a cake" (5/2), even though they represent the same amount. Mixed fractions make it simpler to grasp the actual quantity and compare magnitudes easily.
5. Is it possible to convert an improper fraction directly into a proper fraction?
No, this is a common misconception. An improper fraction cannot be converted into a proper fraction. By definition, an improper fraction represents a value of 1 or more, while a proper fraction always represents a value less than 1. An improper fraction can only be converted into a mixed fraction (a whole number plus a proper fraction) or a whole number if the division has no remainder.
6. Where are mixed fractions more commonly used than improper fractions in real life?
Mixed fractions are used extensively in everyday situations where whole units and parts of units need to be communicated clearly. Examples include:
Cooking: Recipes frequently use measurements like "1 ¾ cups of sugar."
Measurement: A carpenter might measure a plank of wood as "3 feet 5 ½ inches."
7. How do you convert a mixed fraction back into an improper fraction?
To convert a mixed fraction back into an improper fraction, you follow a simple formula: (Whole Number × Denominator) + Numerator. The result becomes the new numerator, and the denominator stays the same. For example, to convert 4 ⅜:
Multiply the whole number (4) by the denominator (8): 4 × 8 = 32.
Add the original numerator (3) to this result: 32 + 3 = 35.
Place this sum over the original denominator: 35/8.
8. For arithmetic operations like multiplication, is it better to use improper fractions or mixed fractions?
For performing arithmetic operations, especially multiplication and division, it is significantly easier and more reliable to first convert any mixed fractions into improper fractions. Working with a single numerator and denominator (as in an improper fraction) simplifies the calculation process and reduces the chances of making errors, which can occur when trying to multiply whole numbers and fractions separately.























