Difference Between Theorem, Lemma, and Corollary

In this article, we are going to talk about theorems, lemmas, and corollary; theorems are those mathematical statements which are true and have logical proof. For example, De Moivre’s Theorem, Alternate Segment Theorem, etc. In this article, we are going to talk about how to prove different theorems and also solve some questions based on them. A corollary is a statement that follows naturally from some other statement that has either been proven or is generally accepted as true. For example, The sum of the interior angles of any triangle is always 180 degrees. A lemma is like a mini-theorem that helps you prove a bigger theorem or statement. For example, Euclid’s Division Lemma.

Table of Contents

• An Overview of Theorems, Lemma, and Corollary

• History of the Mathematician

• Definition of Theorem

• Statement of De Moivre’s Theorem

• Proof of De Moivre’s Theorem

• Definition of Lemma

• Definition of Corollary

• Solved Examples

• Important Points to Remember

History of Euclid 

Euclid

Image Credit: Wikimedia

Name: Euclid

Born: Mid-4th century BC

Field: Mathematics

Contribution: Euclid was the very first person to start discovering these theorems and Lemma.

Nationality: Greek

Definition of Theorem

A theorem is a mathematical statement that is true and has very logical proof. It can either be for algebra or geometry, but the result of a theorem can always be proved.

Let us take the example of De Moivre’s Theorem to explain how a theorem can be proved.

Statement of De Moivre’s Theorem

According to the De Moivre Theorem, if we raise the power of a polar complex number by n, then it is equivalent to increasing the modulus to the same power and multiplying it by the argument raised to the same power, which means:

${{(\cos x+\sin x)}^{n}}=\cos (nx)+\sin (nx)$.

Proof of De Moivre’s Theorem

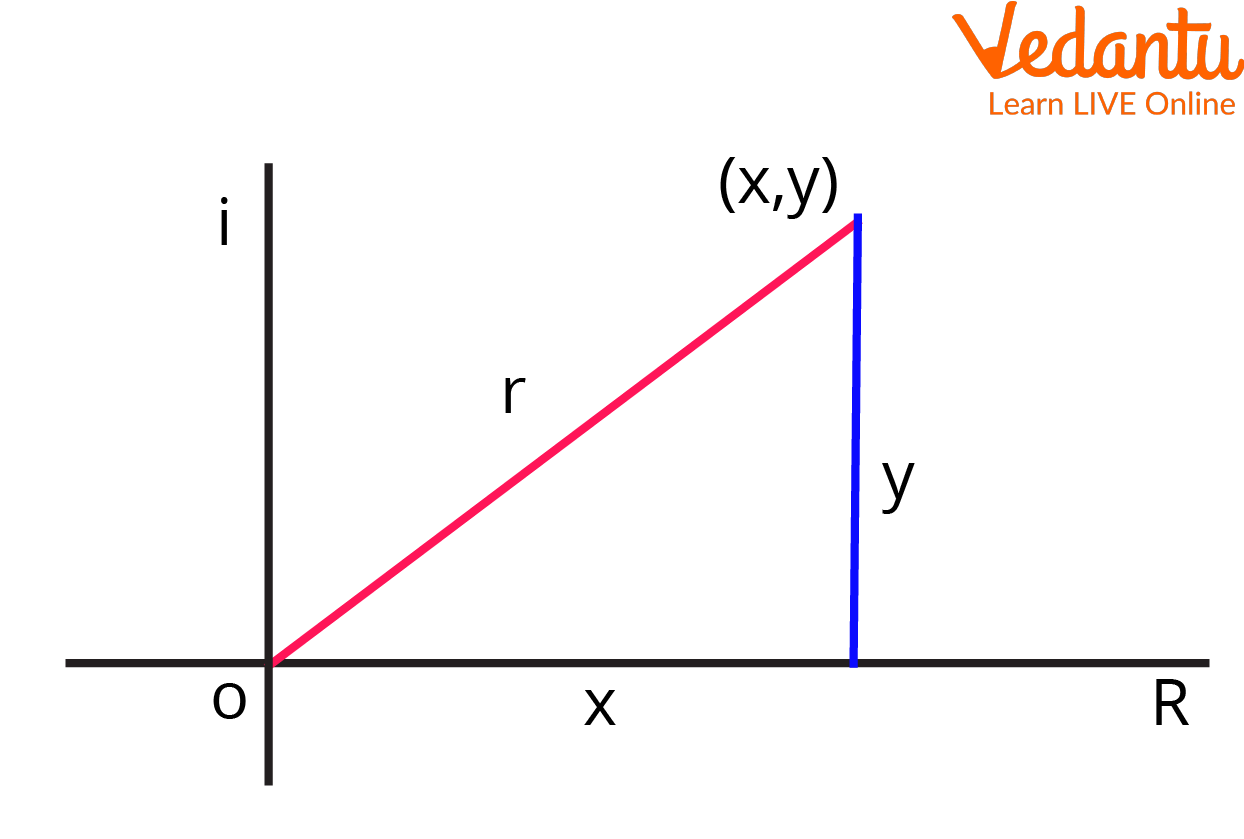
Let us take a complex number $z=x+iy$. This complex number can be written in polar form as $z=r(\cos \theta +i\sin \theta )$.

Here, $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ ($r$ is called the modulus/absolute value of the complex number).

When we plot the complex number on the argand plane:

Argand Plane

$\cos \theta =\dfrac{x}{r}$ 

$\sin \theta =\dfrac{y}{r}$ 

Now, let’s raise the complex number $z$ to the power $n$.

$z=r(\cos \theta +i\sin \theta )$

${{z}^{n}}={{(r(\cos \theta +i\sin \theta ))}^{n}}$

${{z}^{n}}={{r}^{n}}{{(\cos \theta +i\sin \theta )}^{n}}$

Solving using the principle of mathematical induction:

For $n=1$

${{(\cos \theta +i\sin \theta )}^{1}}=\cos (1\theta )+\sin (1\theta )$

Assuming this to be true for $n=k$,

${{(\cos \theta +i\sin \theta )}^{k}}=\cos (k\theta )+\sin (k\theta )$

Proving this to be true for $n=k+1$,

${{(\cos \theta +i\sin \theta )}^{k+1}}={{(\cos \theta +i\sin \theta )}^{k}}.{{(\cos \theta +i\sin \theta )}^{1}}$

${{(\cos \theta +i\sin \theta )}^{k+1}}=(\cos (k\theta )+i\sin (k\theta )).(\cos \theta +i\sin \theta )$

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos (k\theta ).\cos (\theta )+i\cos (k\theta ).\sin \theta +i\sin (k\theta )\cos (\theta )-\sin (k\theta )\sin (\theta )$

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos (k\theta ).\cos (\theta )-\sin (k\theta )\sin (\theta )+i(\cos (k\theta ).\sin \theta +\sin (k\theta )\cos (\theta ))$

Using trigonometry formulae:

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos (k+1)\theta +i(\sin (k+1)\theta )$

Hence Proved.

Definition of Lemma

A lemma is nothing but a proven statement that is used to prove other statements. Lemma is like a mini-theorem that helps you prove a bigger theorem or statement.

A few examples of a lemma are as follows:

Euclid’s Division Lemma - According to Euclid's division lemma, we will always get a unique integer as the quotient and a unique integer as the remainder when we divide one integer by another non-zero integer. The theorem states that, for given two positive integers, $a$ and $b$, there exist unique integers, $q$ and $r$, such that $a=bq+r$, where $0\le r<b$. The integer $q$ is the quotient and the integer $r$ is the remainder. The quotient and the remainder are unique.

Definition of Corollary

The corollary is a statement that follows with little or no proof required from an already proven statement. For example, there is a theorem in geometry that the angles opposite to two congruent sides of a triangle are also congruent. A corollary to this statement is that an equilateral triangle is equiangular.

So for a corollary, the proof relies heavily on a given certain theorem. A corollary can be proved but it depends on some theorem heavily. There can't be any assumptions in the proof.

Solved Examples

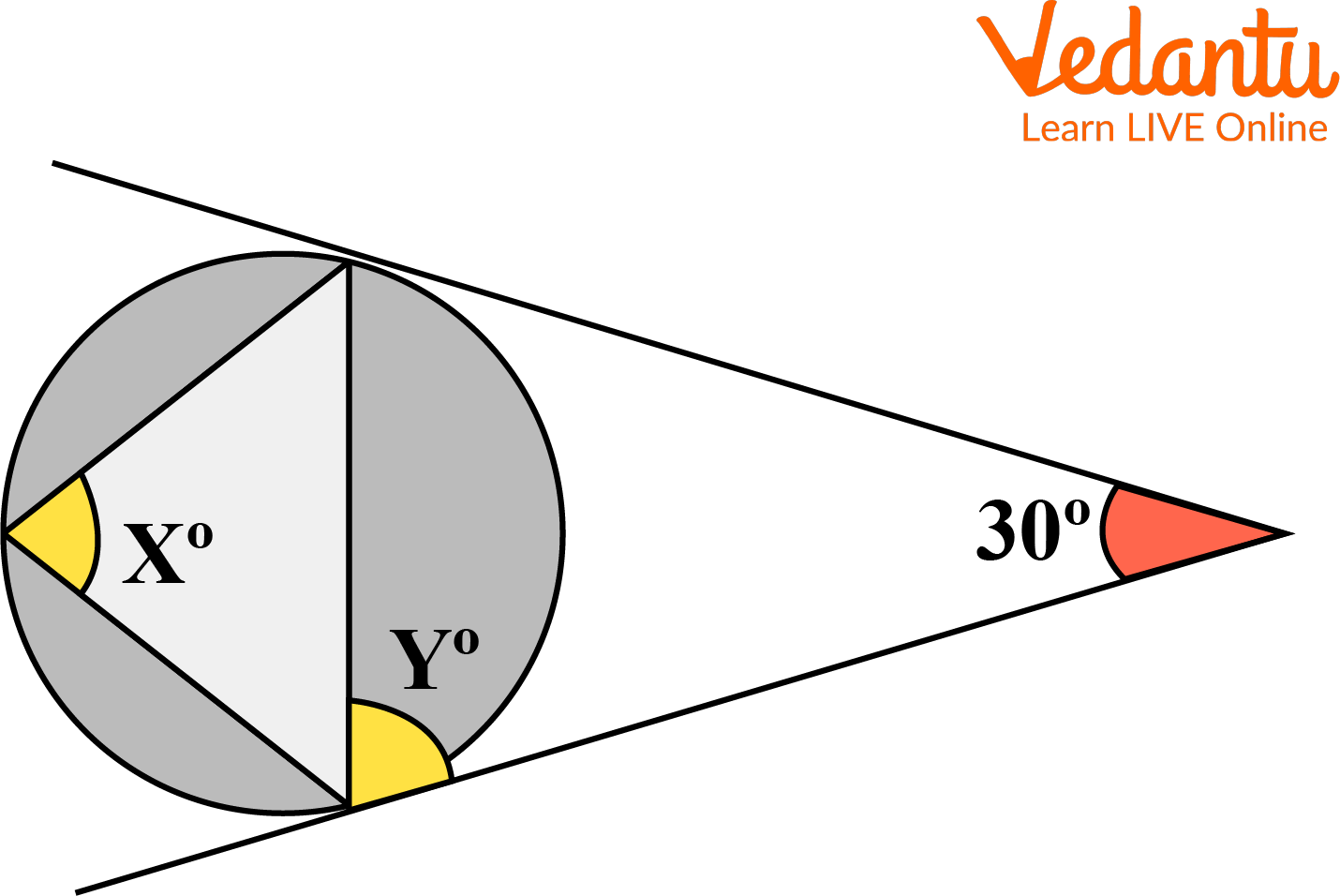
1. Find \[X{}^\circ +Y{}^\circ \].

A Circle with Two Tangents

Ans. Here, \[\angle Y\] is the angle between the chord and the tangent and \[\angle X\] is the angle subtended at the circumference by the chord in the alternate segment.

Hence, \[\angle X=\angle Y\].

\[\angle X\] and \[30{}^\circ \] are the opposite angles of a cyclic quadrilateral:

\[\angle X+30{}^\circ =180{}^\circ \]

\[\angle X=150{}^\circ \]

\[\angle Y=150{}^\circ \]

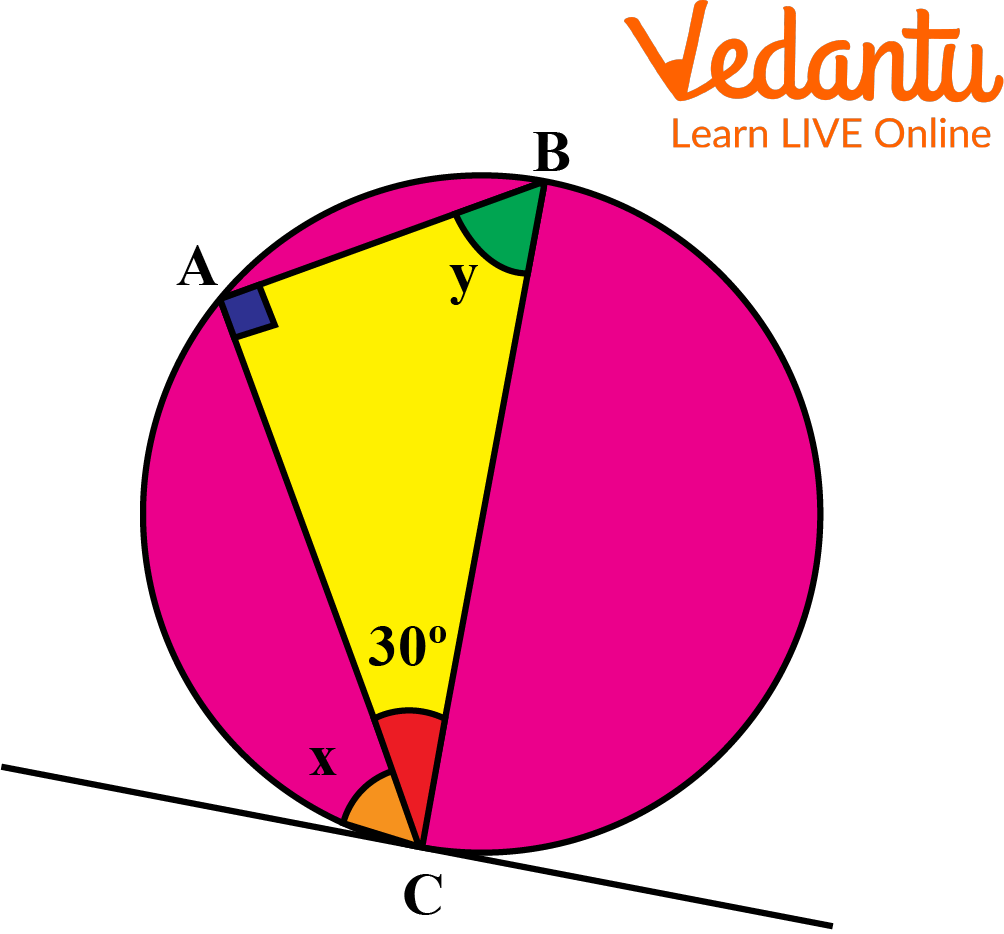
2. Calculate the value of angles x and y in the given diagram.

A Circle

Ans. The tangent to the circle has the point of contact at \[C\], the angle formed between the tangent and the chord \[AC\] is \[\angle x\] and the chord \[AC\] is subtending an \[\angle y\] in the alternate segment of the circle.

\[\angle x=\angle y\] (Alternate Segment Theorem)

\[\angle ABC+\angle BAC+\angle ACB=180{}^\circ \](Angle sum property of Triangle)

\[\angle y+90+30=180\]

\[\angle y+120=180\]

\[\angle y=60{}^\circ \]

3. Find DE

Ans. According to the basic proportionality theorem:

\[\frac{AE}{DE}=\frac{BE}{CE}\] 

\[\frac{4}{DE}=\frac{6}{8.5}\]

\[\frac{4*8.5}{6}=DE\]

\[DE=5.66\]

Important Points to Remember

• Lemma is nothing but just a follow-up of a theorem, it helps us in proving bigger theorems.

• The corollary is an idea developed from a theorem that is already proved; here, the word idea means understanding the same theorem differently to try to prove another theorem.

List of Related Articles

• Euclid Division Lemma

• Bayes Theorem