Estimating Quotient

A quotient is a number calculated by dividing one integer by another.

For example, dividing 10 slices of cake among 5 children yields 2 slices of cake, implying that each child receives 2 slices of cake. In this case, 2 is referred to as the quotient. This is expressed numerically as

\[10 \div 5 = 2\]

10 is the dividend, 5 is the divisor, 2 is the quotient, and \[ \div \] is the division sign. Here we estimated that if 10 slices are there for 5 children, then each will get 2 slices. If we reduce this number to 9 slices, then one child would only get one cake slice and not two.

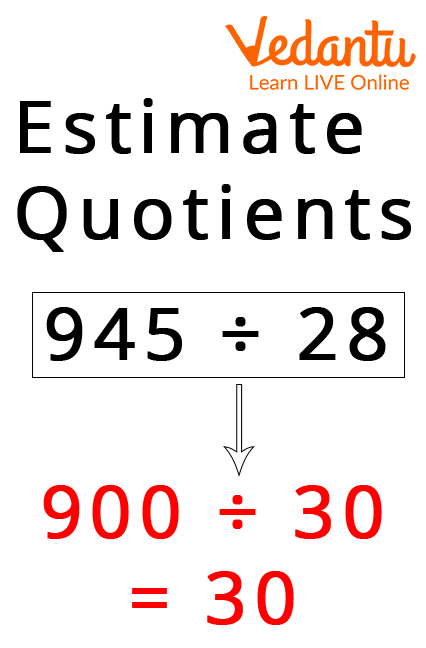
Estimating Quotient By Round-Off

What is an Estimating Quotient?

Obtaining a result near the accurate or actual outcome is referred to as estimation. It means coming to certain conclusions or rounding a figure to the closest decimal place or ones, tens, hundreds, and so on.

Estimation may be necessary for a variety of reasons. It is useful when there is insufficient information to determine a precise number. When calculating transaction amounts, accountants make estimations. We round the payout to the closest tens, hundreds, or thousands to calculate the quotient.

There are three ways to calculate the quotient:

• Estimate Quotients using Compatible Numbers

• Estimate Quotients Using Multiples

• Estimate the Quotient by Rounding

Estimating Quotient Using A Compatible Number

Compatible numbers are easily divided. Such numbers are closer to the equal value of the actual numbers, making estimation and problem-solving easier. We can round the complex number to the nearest tens, hundreds, thousands, ten thousand, and so on to make them compatible. For example, 48 can be rounded off as 50, and 887 can be rounded off as 890 to make them compatible.

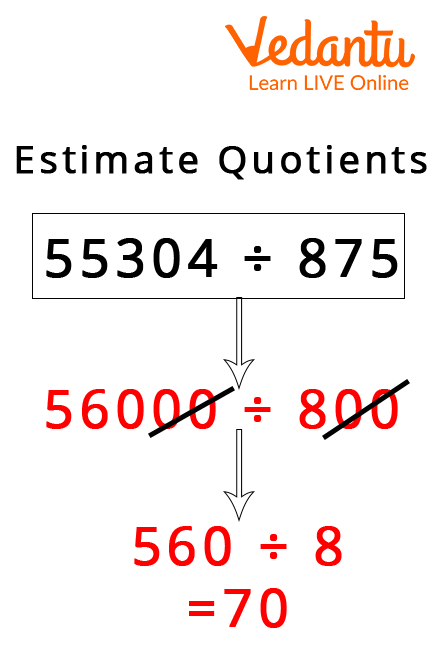
Example Of Estimating Quotient Using Compatible Number

Estimating Quotient Using The Rounded Number

Estimation can be used to compare the assumed quotient to the exact quotient value. We can decide whether or not an answer to a division issue is reasonable. In other words, we can approximate the precise quotient between two integers. This requires determining two-rounded dividend figures that are easily divisible. The roundoff rule can be used depending on the size of the number. The numbers can be rounded to the closest 10, 100, 1000, and so on. For example, if we want to divide 7898 by 9, then we can round off 7898 to 8000 and 9 to 10 to make calculations easy, and hence we can estimate the quotient.

Estimating Quotient Using The Multiples

To estimate quotients in a division question, divide by multiples of different numbers.

To get the quotient, we must first examine the first two or more digits of the dividend based on the divisor and then use the fundamental division facts.

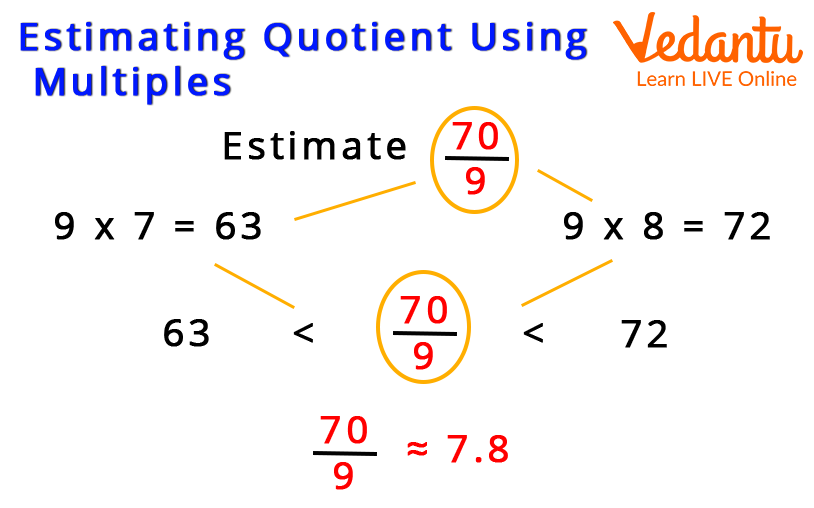
Example of Estimating Quotient Using Multiples

Conclusion

Estimating the quotient makes it easier to calculate by using straightforward steps. The quotient can be estimated by rounding the numbers to 10, 100 or 1000. It can also be estimated by using the divisor's multiple based on the dividend's digits. Estimating the quotient makes the calculation very easy.

Sample Questions

1. Estimate the quotient of 840 \[ \div \] 92.

Ans: The nearest 10’s of 92 is 90, and 840 already has zero present at the end. Now, if we remove the zeroes of both numbers, we are left with 84 and 9. As 9 times 9 is 81, the closest number to 84, our quotient would be near 9.

2. Estimate the quotient of 627 \[ \div \] 23.

Ans: Both the numbers can be changed into near tens and hundreds. So, 23 would become 20 and 627 would become 600 by rounding them off. Now dividing the numbers 600 and 20, we get the quotient as 30. So dividing 627 by 23, we will get a quotient near 30.

3. Estimate the quotient of 136 \[ \div \] 6.

Ans: Estimating quotient using multiples, we can think of multiples of 6, which will result in a value near 136. As 6\[ \times \]10 is 60, 6\[ \times \]20 is 120, and 6\[ \times \]25 is 150. 136 lies between 120 and 150 and is closest to 150, so the estimated quotient would be almost 23.