The Factor of 175

A factor is a number that completely divides the original number. Real numbers that can evenly divide the original number are factors of $175$. There is no residue if $"x"$ is the factor of $175$, since $"x"$ divides $175$ into equal parts. For instance, $24$ divided by $4$ is $6$, then 4 is the component of $24$. Consequently, $4$ divides $24$ into six equal parts, leaving $0$ as the remainder. Since $175$ can only be divided by $1,5,7,25,35and175$. So these are factors of 175.

Let's use straightforward methods in this article to determine the factors, pair factors, and prime factors of $175$.

What are the Factors of $175$?

The natural numbers that can divide the number $175$ evenly are factors of $175$. These factors divide the original number into equal numbers of parts. For example, $175$ is divisible by $5$. So, $175$ divided by $5$ is equal to $35$. Hence, $5$ divides the number $175$ into $35$ equal parts.

We can determine the other factors of $175$ with the help of the division method. $175$ has more than two factors. Thus, it is a composite number.

How to Find Factors of $175$?

The natural numbers that can divide the number $175$ evenly are factors of $175$. So the way you find and list all of the factors of $175$ is to go through every number up to and including $175$ and check which numbers result in an even quotient.

In the division method, the factors of $175$ are found by dividing the number $175$ by different integer numbers. If the integer divides $175$ exactly without leaving a remainder, then the integer is a factor of $175$. Let's start dividing $175$ by $1$ and proceed with the different integers.

$175÷1=175$

$175÷2=87.5$ So, 2 is not a factor of 175.

$175÷5=35$

$175÷7=25$

$175÷25=7$

$175÷35=5$

$175÷175=1$

Therefore, the factors of $175$ are 1, 5, 7, 25, 35 and 175.

Prime Factorisation of $175$

Prime factorization is the process of finding the prime terms or prime factors which, when multiplied, give the original number.

Prime Factorization of 175

Take a pair factor of $175$, say $(1,175)$

As the number $1$ is neither prime nor composite, it cannot be split further. Take the other factor, $175$, which is a composite number, and it can be factored further into its prime factors.

Thus, $175$ is written as the product of $7$ and $25$. Here, $7$ is a prime number, $25$ is a composite number, and the number $25$ can be written as the product of $5and$5.

Write the number $175$ as the product of its prime factors.

So, $175$ is written as $5\times 5\times 7$.

Therefore, the prime factorization of $175$ is $5\times 5\times 7$ or $5^2\times 7$, where $5$ and $7$ are prime numbers.

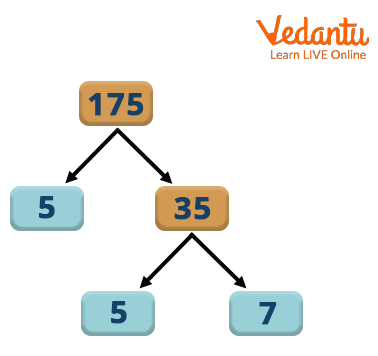
Factor Tree

Pair Factors of $175$

A factor pair is a pair of numbers that, when multiplied, will result in an original number(or the same product).

To calculate the factor of a number, factors are frequently presented as pairs of numbers. They are referred to as factor pairs. For example- factor pairs of $12$ include, $(1,12)$ and $(3,4)$.

The pair factors of $175$ are expressed in positive and negative forms. Since the number $175$ is composite, it has more than one-factor pair. Thus, the positive and negative pair factors of $175$ are given below:

Positive Pair Factor of $175$:

$1\times 175=175$

$5\times 35=175$

$7\times 25=175$

Therefore, the positive pair factors of $175$ are $(1,175)$, $(5,35)$ and $(7,25)$.

Negative Pair Factor of $175$:

$-1\times -175=175$

$-5\times -35=175$

$-7\times -25=175$

Therefore, the negative pair factors of $175$ are $(-1,-175)$, $(-5,-35)$ and $(-7,-25)$

Prime Factors of $175$

First, note that prime numbers are all positive integers that can only be evenly divided by $1$ and itself. Prime Factors of $175$ are all the prime numbers that, when multiplied together, equal $175$.

All the prime numbers used to divide in the Prime Factor Tree are the Prime Factors of $175$. Here are the maths to illustrate:

$175÷5=35$

$35÷5=7$

$7÷7=1$

Again, all the prime numbers you used to divide above are the Prime Factors of $175$. Thus, the Prime Factors of $175$ are $5,7$.

Solved Examples

Example 1: What are the possible factors of $175$?

Solution: The natural numbers that can divide a number evenly are factors of $175$. As a result, the factors of the $175$ are $1,5,7,25,35and175$. If we divide $1755$ by any negative of these integers, then the resulting number will always be a factor of 175. Generally, we consider only positive numbers as factors.

Example 2: Can you assist Aman with adding up all the factors of $175$?

Solution: First, we must take out the factors of $175$.

$175=1,5,7,25,35,175$

Here we can see the $1755$ are $1,5,7,25,35and175$.

We can conclude here that If you add up all the components of $175$,

you get $1+5+7+25+35+175=248$

Example 3: Is $25$ a factor of $175$?

Solution: Yes, $25$ is a factor of $175$. If $175$ is divisible by $25$, it leaves a quotient of $7$ and remainders $0$. Hence, $25$ is a factor of $175$.

Conclusion

The number $175$ is odd and composite in mathematics. The only numbers with more than two elements are composite. Each factor is either less than or equal to the original number. A given integer has a finite number of factors. Factors of $175$ are numbers that leave no residue when divided by $1,5,7,25,35and175$.