Factors of 52: An Introduction
A factor of an integer is another integer that can divide the integer without leaving any remainder. Every number greater than one has at least two factors. So, the factors of 52 are the numbers that divide 52 exactly with no remainder. Prime factorization of a number is calculated by dividing the given number by its prime factors and keeping on dividing by prime factors till we get 1 as the quotient. We know that a composite number includes more than two factors. Thus, this method applies only to composite numbers instead of prime numbers. Hence, the factors of 52 are 1, 2, 4, 13, 26, and 52.
What Are The Factors of 52?
The factors of 52 are the numbers that divide 52 exactly without leaving the remainder. Since the number 52 is an even composite, it has many factors other than 1 and 52. Hence, the factors of 52 are 1, 2, 4, 13, 26, and 52.
Finding Factors of 52
The factors of 52 are the numbers that divide 52 exactly with no remainder. 52 is a composite number, so it has more than two factors. The way you find and list all of the factors of 52 is to go through every number up to and including 52 and check which numbers result in an even quotient (which means no decimal place). To determine the factors of 52, follow the below steps.
Identify the numbers that divide 52 with a remainder 0.
\[52\div 1=52\]
1 is a factor of 52.
\[52\div 2=26\]
2 is a factor of 52.
\[52\div 4=13\]
4 is a factor of 52.
\[52\div 13=4\]
13 is a factor of 52.
\[52\div 26=2\]
2 is a factor of 52.
\[52\div 52=1\]
52 is a factor of 52.
Hence, the factors of 52 are 1, 2, 4, 13, 26, and 52.
Factor Pairs of 52
Pair factors may be positive or negative, but they cannot be a fraction or a decimal. To get the factor pairs of 52, multiply the two numbers in a pair to obtain the original number, which is 52, as follows:
Positive Factors of 52
Thus, the positive pair factors are \[\left( 1,\text{ }52 \right),\text{ }\left( 2,\text{ }26 \right)\] and \[\left( 4,\text{ }13 \right)\].
Negative Factors of 52
Thus, the negative pair factors are \[\left( -1,\text{ }-52 \right),\text{ }\left( -2,\text{ }-26 \right)\] and \[\left( -4,\text{ }-13 \right)\].
Prime Factorization of 52 by The Division Method
Prime factorization of 52 refers to determining the prime factors of 52. Divide 52 by the smallest prime number possible to get the prime factor of 52. Then, take the result and divide it by the lowest prime number. Repeat this step until we have 1.
Step 1: Divide 52 by 2
\[52\div 2=26\]
Step 2: Again divide 26 by 2
\[26\div 2=13\]
Step 3: Divide 13 by 13
\[13\div 13=1\]
Thus, we get 1 at the end of this division method, and we can’t go on with the division approach. Hence, the prime factor of 52 is \[2\times 2\times 13\] or \[{{2}^{2}}\times 13\], where 2 and 13 are prime numbers.
Factor Tree of 52
Factor trees represents the factors of a number, especially its prime factorization. We should also remember that 1 is not a prime number; thus, it will not appear in any factor tree.
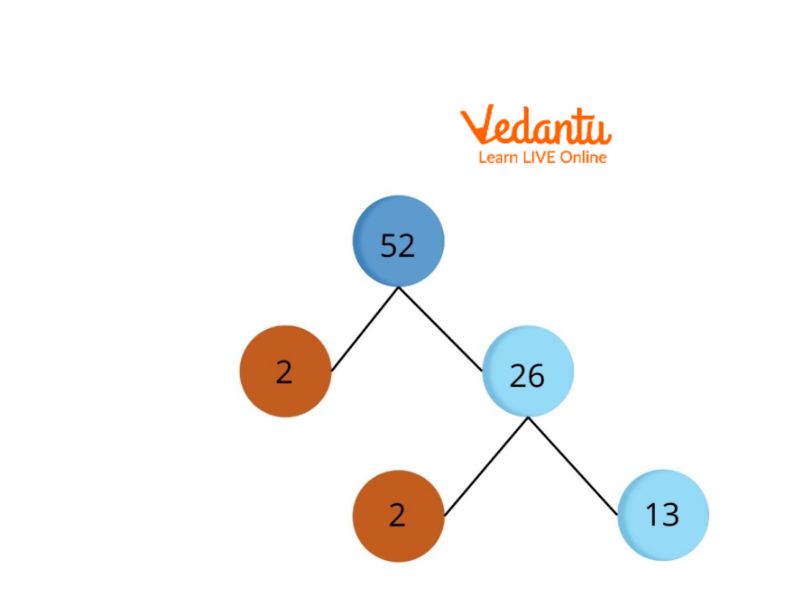
Factor Tree of 52
Interesting Facts
Every number has at least two factors which are one and the number itself
We know that 52 is a composite number as it has more than two factors
Important Questions
1. What is the pair factor of 62?
Ans: A factor pair is a pair of numbers that, when multiplied together, provide a certain product or the same product. To get the pair factor of 62, multiply the two numbers in a pair to obtain the original number, which is 62.
Thus, the positive pair factors are \[\left( 1,\text{ }62 \right)\] and \[\left( 2,\text{ }31 \right)\] and the negative pair factors are \[\left( -1,\text{ }-62 \right)\] and \[\left( -2,\text{ }-31 \right)\].
2. Draw a factor tree for 58.
Ans: Factor trees represent the factors of a number, especially its prime factorization. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops. We should also remember that 1 is not a prime number; thus, it will not appear in any factor tree. Thus, the prime factorization of 58 is \[2\times 29\].
Factor Tree of 58
3. What is the prime factorization of 42?
Ans: Prime factorization of a number is calculated by dividing the lowest prime factor of the given number and keeps on dividing by prime factors till we get 1 as the quotient.
Thus, the prime factorization of 42 is \[2\times 3\times 7\], where 2, 3 and 7 are prime numbers.
Summary
In this article, we learned about the factors of 52, as well as prime factors of 52, the pair factors of 52, and how to find the factors of 52 using the prime factorization method with solved sums. Hence, all factors of 52 are 1, 2, 4, 13, 26, and 52 and the prime factors of 52 are \[2\times 2\times 13\] where 2 and 13 are prime numbers.
Practice Questions
1. How many factors does 52 have?
5
6
8
10
Ans: Option B
2. Is 52 a composite number?
Yes
No
Ans: Option A
FAQs on How to Find Factors of 52?
1. Can we find the prime factors of 5?
Yes. Prime factorization of 5 refers to determining the prime factors of 5. A prime factor is a multiplicand that is a prime number and not a composite one. We know that 5 is a prime number. Because 5 is divisible by only itself. Therefore, only the number 5 itself is a prime factor in it.
2. Does a number have negative factors?
The pair factors might have both positive and negative values. The pair factors of 44, for instance, might be \[\left( 1,\text{ }44 \right)\] or \[\left( -1,\text{ }-44 \right)\]. When two negative numbers are multiplied, such as when \[-1\] and \[-44\] are multiplied, the answer is 44.
3. Can 1 be a factor of all numbers?
Yes. Every number has a factor of 1 because when one divides a number exactly, leaving no remainder, the result is the number itself.
Eg: \[9\div 1=9\]
1 is a factor of 9.
