Introduction to Hypotenuse Leg Theorem
The longest side of a right-angled triangle, known as the hypotenuse, is always opposite to the right angle. According to the hypotenuse leg theorem, two right triangles are congruent if the hypotenuse and one leg of one right triangle coincide with the hypotenuse and leg side of the second right triangle. We employ the HL (Hypotenuse Leg) Theorem or the RHS (Right angle-Hypotenuse-Side) congruence rule to demonstrate the congruence of any two right triangles. In this article, we'll study more about the hypotenuse leg theorem.
Table of Contents
Introduction to Hypotenuse Leg Theorem
What is the Hypotenuse Leg Theorem?
Hypotenuse Leg Theorem Proof
Hypotenuse Leg Theorem Formula
Hypotenuse Leg Theorem Examples
What is the Hypotenuse Leg Theorem?
The hypotenuse leg theorem states that if one right triangle's hypotenuse and one of its legs are congruent with the other right triangle's hypotenuse and one of its legs, the two triangles are congruent. In other words, a collection of right triangles is said to be congruent if the hypotenuse and one leg of each triangle have the same length.
Hypotenuse Leg Theorem Formula
Consider following two right-angled triangles,
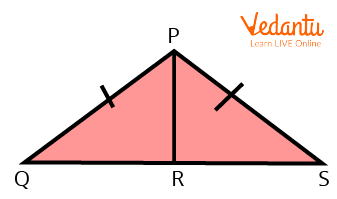
Right-Angled Triangles
By Hypotenuse Leg theorem,
If, \[\;PQ\; = \;PS\] (Hypotenuse)
\[PR\; = \;PR\] (Common side)
Therefore,
$\triangle PQR \cong \triangle PSR$
Hypotenuse Leg Theorem Proof
The hypotenuse leg theorem's proof demonstrates how a set of right triangles are congruent if the lengths of one of their associated hypotenuses and legs are the same. Look at the isosceles triangle ABC below, where the side \[AB\; = \; AC\] and AD is perpendicular to BC.
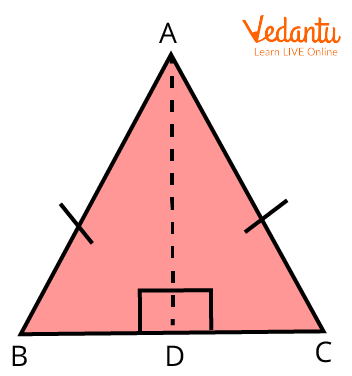
Hypotenuse Leg Theorem Proof
As an altitude, AD is perpendicular to BC and creates the right-angled triangles ADB and ADC. These triangles' respective hypotenuses, AB and AC, are equal.
Therefore, \[AB\; = \;AC\]
Due to their shared presence in both triangles, \[AD\; = \; AD\]
AD is common in both triangles.
Therefore, a hypotenuse and a pair of legs in two right triangles satisfy the hypotenuse leg theorem's definition.
Angles B and C are equal, as we know (Isosceles Triangle Property).
We are also aware of the equality of BAD and CAD angles. (BC is divided in half by AD, making BD equal to CD.)
Consequently,
Therefore, $\triangle ADB \cong \triangle ADC$.
Hence proved.
Applications of Hypotenuse Leg Theorem
The Hypotenuse leg theorem is a theorem that can be applied to demonstrate how two right triangles can be congruent.
The theorem can also be applied to prove the equality of any two right triangles' two sides.
Hypotenuse Leg Theorem Examples
1. Prove that $\triangle ABD \cong \triangle DBC.$ If $\angle A = \angle C = 90^{\circ},$ and \[AD\; = \;BC\].
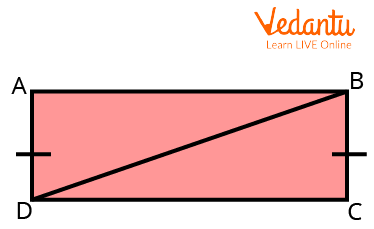
A Rectangle
Ans. We have,
\[AD\; = \;BC\] (equal leg)
\[\angle A = \angle C\] (right angle)
\[BD\; = \;DB\] (common side, hypotenuse)
By the Hypotenuse-Leg theorem,
$\triangle ABD\cong \triangle DBC$
Hence proved.
2. Let's assume that \[\angle W\; = \;\angle Z\; = \;90\;^\circ \], and M is the intersection of WZ and XY. Demonstrate the congruence of the two triangles, WMX and YMZ.
Combination of Triangles
Ans. Given that both $\triangle WMX$ and $\triangle YMZ$ have an angle of \[90^\circ \], they are right triangles (right angles)
\[WM\; = \;MZ\] (leg)
\[XM\; = \;MY\;\](Hypotenuse)
Consequently, according to the Hypotenuse-Leg theorem, $\triangle WMX$ and $\triangle YMZ$ are congruent.
3. Find the value of \[x\] and \[y\] for the given triangles, assuming that $\triangle ABC$ and $\triangle PQR$ are congruent to each other?
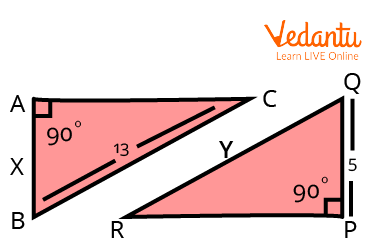
Two Triangles
Ans. By the Hypotenuse-Leg theorem,
In $\triangle ABC$ and $\triangle PQR$,
\[BC\; = \;QR\] (congruent hypotenuse)
Consequently, \[y\; = \;13\;,\;AB\; = \;PQ\] (congruent legs)
Thus, \[x\; = \;5\].
Thus, \[x\; = \;5\] and \[y\; = \;13\].
Conclusion
This article covered the Hypotenuse-Leg theorem and its proof in considerable detail. As a result of the discussion above regarding the Hypotenuse-Leg theorem, it is clear that if the sides and hypotenuse of any two triangles are equal, then the triangles must be congruent. The congruence of triangles and missing sides can be determined using this theorem.
The hypotenuse and one leg are the components that are used to test the congruence of triangles following the Hypotenuse-Leg Congruence rule.
The SAS (Side-Angle-Side) postulate and the Hypotenuse-Leg Congruence rule are related. The main distinction is that the Hypotenuse-Leg theorem uses the right angle, which is not the included angle between the hypotenuse and the leg, as the known angle. In contrast, SAS needs two sides and an added angle.
Related Links:
FAQs on Hypotenuse Leg Theorem
1. What distinguishes the triangle's legs from its hypotenuse?
In a right-angled triangle, the side opposite to the right angle is known as the hypotenuse whereas the other two adjacent sides are known as its legs. The triangle's hypotenuse is always its longest side on the other hand the legs are always shorter. The Pythagorean theorem, which asserts that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides, can be used to calculate the hypotenuse's length.
2. How many triangle congruence theorems are there, and how does the hypotenuse leg theorem differ from them?
A triangle's congruence can be established using the triangle congruence theorem or triangle congruence criteria. The five triangle congruence theorems are Side Side Side, Side Angle Side, Angle Side Angle, Angle Angle Side, and Right Angle-Hypotenuse-Side, often known as the Hypotenuse Leg Theorem. The SAS (Side-Angle-Side) postulate and the hypotenuse leg theorem are similar. The only distinction is that the HL theorem uses the right angle, which is not the included angle between the hypotenuse and the leg, as the known angle, whereas SAS needs the included angle and two sides.
3. Why is it that the hypotenuse theorem only applies to right triangles?
The term "hypotenuse" refers to a right-angled triangle's longest side compared to the base and perpendicular lengths. The right angle, the largest angle of the three angles in a right triangle, is opposite the hypotenuse side. Since the total of the interior angles in a right triangle is always 180 degrees, the right angle must be the largest in the triangle, and the side opposite it must always be the longest. Fundamentally, only the right triangle possesses the hypotenuse property, not any other triangles and hence the hypotenuse theorem only applies to right triangles.
