Mathematical Theorems

In this article, we will cover some important Mathematical Theorems and their Proofs. Those mathematical statements which are true and have a logical proof are called theorems. In this article, we will be discussing statement, proof , applications and limitations of some important theorems in the field of Mathematics. We will also solve some examples at the end. Some Theorems in math examples are  De Moivre’s Theorem, Alternate Segment Theorem, etc.

List of Mathematical Theorems :

• De-Moivre’s Theorem

• Burnside Theorem

• Alternate Segment Theorem

• Lagrange’s Mean Value Theorem

Table of Contents

• Introduction

• History of Euclid

• Statement of De Moivre’s Theorem

• Proof of De Moivre’s Theorem

• Applications of the Theorem

• Solved Examples

• Statement of the Lagrange Mean Value Theorem

• Proof of the Theorem

• Applications of the Theorem

History of Euclid

Euclid

Image Credit: Wikimedia

Name: Euclid

Born: Mid-4th century BC

Field: Mathematics

Contribution: Euclid was the very first person to start discovering these axioms and theorems.

Statement of De Moivre’s Theorem

According to the De Moivre Theorem, if we raise the power of a polar complex number by n, then it is equivalent to increasing the modulus to the same power and multiplying it by the argument raised to the same power.

Proof of De Moivre’s Theorem

Let us take a complex number $z=a+ib$

This complex number can also be represented in polar form as $z=r(\cos \theta +i\sin \theta )$

$r=\sqrt{{{a}^{2}}+{{b}^{2}}}$

(magnitude i.e distance from 0)

$\cos \theta =\frac{a}{r}$

$\sin \theta =\frac{b}{r}$

(position of complex number on the unit circle)

Here, $\theta$ is called the principal argument and r is called the modulus or absolute value.

Now, let’s raise the complex number ‘z’ to a power of ‘n’.

${{z}^{n}}={{(r(\cos \theta +i\sin \theta ))}^{n}}$

${{z}^{n}}={{r}^{n}}{{(\cos \theta +i\sin \theta )}^{n}}$

Solving using the principle of mathematical induction:

For $n=1$

${{(\cos \theta +i\sin \theta )}^{1}}=\cos (1\theta )+i\sin (1\theta )$

Assuming this to be true for $n=k$

${{(\cos \theta +i\sin \theta )}^{k}}=\cos (k\theta )+i\sin (k\theta )$

Proving this to be true for \[n\text{ }=\text{ }k+1\]

${{(\cos \theta +i\sin \theta )}^{k+1}}={{(\cos \theta +i\sin \theta )}^{k}}.(\cos \theta +i\sin \theta )$

${{(\cos \theta +i\sin \theta )}^{k+1}}=(\cos (k\theta )+i\sin (k\theta )).(\cos \theta +i\sin \theta )$

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos (k\theta ).\cos \theta +i\cos (k\theta ).\sin \theta +i\sin (k\theta ).\cos \theta -\sin (k\theta ).\sin \theta$

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos (k\theta ).\cos \theta -i\sin (k\theta ).\sin \theta +i(\cos (k\theta ).\sin \theta +\sin (k\theta ).\cos \theta )$

${{(\cos \theta +i\sin \theta )}^{k+1}}=\cos ((k+1)\theta )+i\sin ((k+1)\theta )$

Hence Proved

Diagram of Complex Number in Polar Form

Complex Number in an Argand Plane

The point with coordinates as (x,y) is the complex number represented in the Argand Plane, Ө is the principal argument of the complex number and $r$ is the modulus of the complex number and its value is $\sqrt{{{x}^{2}}+{{y}^{2}}}$.

Limitations of De Moivre’s Theorem

• The first limitation of De Moivre’s Theorem is that it is not applicable to non-integers, the value of n should always be an integer.

• The value of x cannot be an imaginary number, it should always be a real number.

Application of De Moivre’s Theorem

De Moivre’s theorem can also be used to calculate the nth roots of a complex number:

Let a complex number be $z=\cos x+i\sin x$

nth roots of z will be:

${{r}^{(\frac{1}{n})}}(\cos (\frac{x+2k\pi }{n})+i\sin (\frac{x+2k\pi }{n}))$

Here k = 0,1,2……..(n-1)

Important Points

• The value of n should always be an integer.

• The value of Ө will change if the complex number is not lying in the first quadrant.

• The nth root equation can also be used to calculate the roots of unity.

Statement of the Lagrange Mean Value Theorem 

According to the Lagrange mean value theorem, if a function $f$ is continuous over the closed interval $\left[ a,b \right]$ and differentiable over the open interval \[\left( a,\text{ }b \right)\], then there must be at least one point \[c\] in the interval \[\left( a,\text{ }b \right)\] where the slope of the tangent at the point \[c\] equals the slope of the secant through the curve's endpoints.

\[{{f}^{'}}(c)=\frac{f(b)-f(a)}{b-a}\]

Proof of the Theorem

Let the curve be represented as\[f(x)\]:

Let \[g(x)\] be the secant line to f(x) passing through the points (a, f(a)) and (b, f(b)):

Slope (\[g(x)\]) = m = \[\frac{f(b)-f(a)}{b-a}\]

The equation of the secant line will be:

\[y-{{y}_{1}}=m(x-{{x}_{1}})\]

\[y-f(a)=\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.(x-a)\]

\[y=\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.(x-a)+f(a)\]

As we are writing the equation of the secant line, hence:

\[y=g(x)\]

\[g(x)=\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.(x-a)+f(a)\]

Now, let us define a function \[h(x)\] which is the difference between the curve \[f(x)\] and the secant line \[g(x)\].

Hence, , \[h(x)=f(x)-g(x)\]

\[h(x)=f(x)-\left[ \left. \left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.(x-a)+f(a) \right] \right.\]

Now, let us consider that the function \[h(x)\] is continuous on the interval \[\left[ a,b \right]\]  and differentiable on the interval \[\left( a,b \right)\].

If this is the case then there must be a \[c\in \left( a,b \right)\] for which \[{{h}^{'}}(c)=0\]

\[{{h}^{'}}(x)={{f}^{'}}(x)-\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.\]

\[{{h}^{'}}(c)={{f}^{'}}(c)-\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.=0\]

\[{{f}^{'}}(c)=\left( \left. \frac{f(b)-f(a)}{b-a} \right) \right.\]

Hence, the Lagrange mean value theorem is proved.

Applications of the Theorem

• One of the most important applications of the Lagrange Mean value theorem is that it is used to find whether the function is of increasing nature/ decreasing nature.

• It is also used to determine the existence and uniqueness of the roots of an equation.

• It is also used in proving other important equations.

Solved Examples

1. Name some theorems other than De Moivre’s theorem?

Ans.   Names of some other mathematical theorems are:

• Alternate segment theorem

• Basic proportionality theorem

• Binomial theorem

• Bayes theorem

2. What is the Alternate Segment Theorem?

Ans. The angle between a tangent and a chord is equal to the angle in the Alternate Segment Theorem.

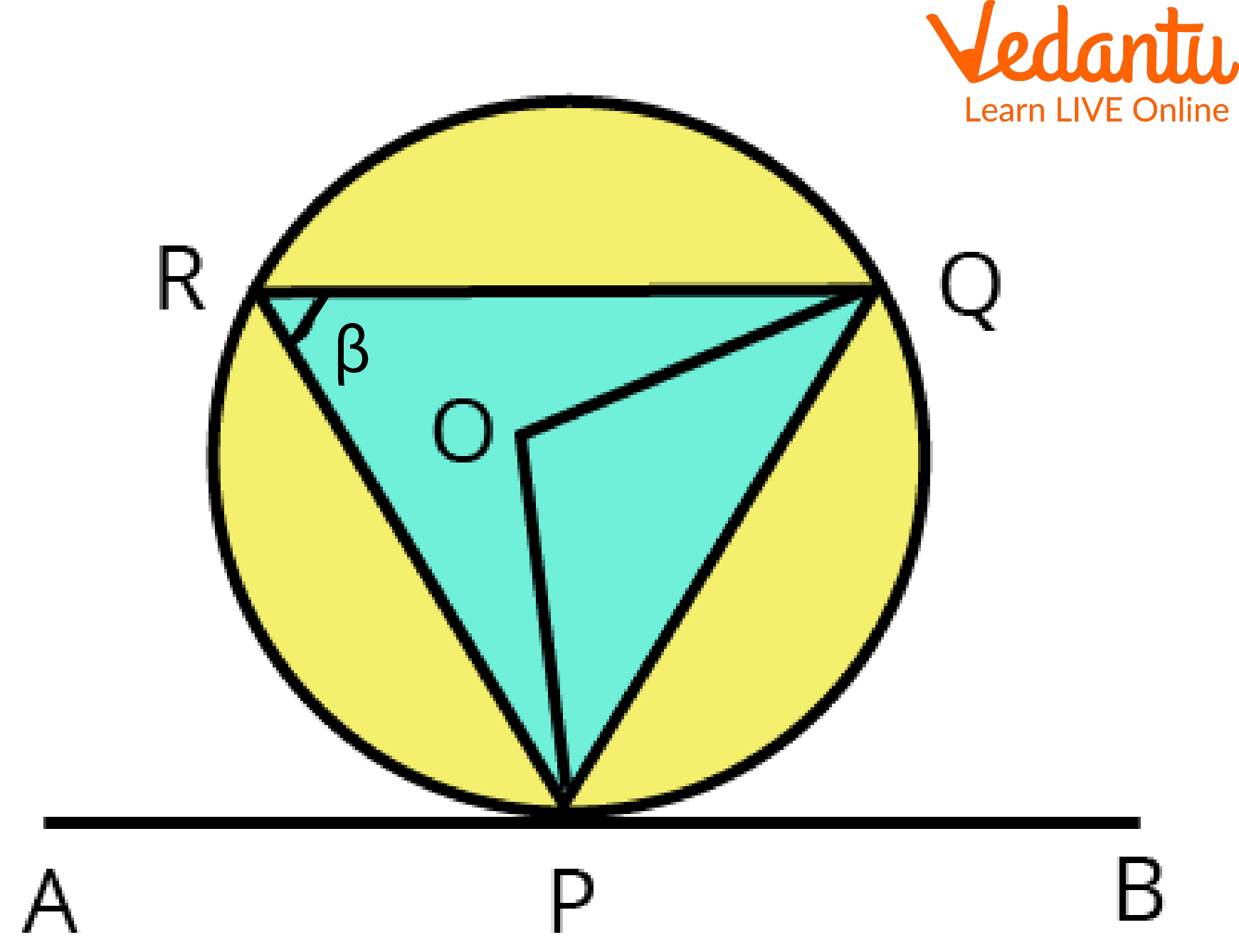
Representation of Alternate Segment Theorem

Hence, according to the definition of the alternate segment theorem $\angle         QPB =\angle \beta $

3. What is the Basic Proportionality Theorem?

Ans. The Basic Proportionality Theorem asserts that if a line is drawn parallel to any one side of a triangle and crosses the other two sides at two different positions, the line splits the other two sides in the same proportion.

Important Points

• According to the De Moivre Theorem, if we raise the power of a polar complex number by n, then it is equivalent to increasing the modulus to the same power and multiplying it by the argument raised to the same power.

• According to the Lagrange mean value theorem, if a function $f$ is continuous over the closed interval $\left[ a,b \right]$ and differentiable over the open interval \[\left( a,\text{ }b \right)\], then there must be at least one point \[c\] in the interval \[\left( a,\text{ }b \right)\] where the slope of the tangent at the point \[c\] equals the slope of the secant through the curve's endpoints.

\[{{f}^{'}}(c)=\frac{f(b)-f(a)}{b-a}\]