Middle Term Formula

The middle-term formula is a formula used to find the middle term of a binomial expansion. Recall that a binomial expansion is an expression involving the sum or difference of two terms raised to some integral power. Depending on the total number of terms, we can write the middle term of that expression.

Definition of Binomial Expansion

A binomial expansion is an expansion of the sum or difference of two terms raised to some power n, where n is a positive integer. The general form of binomial expansion is \[{(a + b)^n}\], where a and b are two algebraic terms with different variables. They may be numbers as well.

Some examples of Binomial Expansion are: \[{(2x + 3y)^5},{(5{x^2}y - 4x{y^2})^3},{(x + {\textstyle{1 \over {2x}}})^{10}}\]and so on.

Binomial Theorem for a Positive Integer n

The Binomial Theorem gives the expansion of a binomial to any positive integral power. It is stated as:

\[{(a + b)^n} = {}^n{C_0}{a^{n - 0}}{b^0} + {}^n{C_1}{a^{n - 1}}{b^1} + {}^n{C_2}{a^{n - 2}}{b^2} + \cdots + {}^n{C_r}{a^{n - r}}{b^r} + \cdots + {}^n{C_n}{a^{n - n}}{b^n}\]. This means that

• There are (n+1) terms in a binomial expansion.

• The compact form of binomial theorem is: \[{(a + b)^n} = \sum\limits_{k = 0}^n {{}^n{C_k}{a^{n - k}}{b^k}} \] .

• The index of the first term, i.e., ‘a’ decreases whereas the index of the second term, i.e., ‘b’ increases as we go from left to right in binomial expansion.

• The coefficients of the terms\[{}^n{C_r}\]are known as Binomial Coefficients.

• For Example, the binomial expansion of \[{(2x + 3y)^5}\] is \[\begin{array}{l}{(2x + 3y)^5} = {}^5{C_0}{(2x)^{5 - 0}}{(3y)^0} + {}^5{C_1}{(2x)^{5 - 1}}{b^1} + {}^5{C_2}{(2x)^{5 - 2}}{b^2}\\ + {}^5{C_3}{(2x)^{5 - 3}}{(3y)^3} + {}^5{C_4}{(2x)^{5 - 4}}{(3y)^4} + {}^5{C_5}{(2x)^{5 - 5}}{(3y)^5}\\ = {(2x)^5} + 5{(2x)^4}{(3y)^1} + 10{(2x)^3}{(3y)^2} + 10{(2x)^2}{(3y)^3} + 5{(2x)^1}{(3y)^4} + {(3y)^5}\\ = 32{x^5} + 240{x^4}y + 720{x^3}{y^2} + 1080{x^2}{y^3} + 810x{y^4} + 243{y^5}\end{array}\]

General Term of Binomial Expansion

The general rth term of a Binomial Expansion \[(a+b)^n\] is denoted by \[{T_{r + 1}} = {}^n{C_r}{a^{n - r}}{b^r}\].

For Example, Given Binomial Expansion \[{(2x + 3y)^5}\], the general term is \[{T_{r + 1}} = {}^5{C_r}{(2x)^{5 - r}}{(3y)^r}\]. If we need to find the third term, equate 3 to r+1, which means

\[r + 1 = 3 \Rightarrow r = 2\]. So,

\[\begin{array}{l}{T_{r + 1}} = {}^5{C_2}{(2x)^{5 - 2}}{(3y)^2} = \dfrac{{5!}}{{2!\left( {5 - 2} \right)!}}{(2x)^3}{(3y)^2}\\ = \dfrac{{5!}}{{2!\left( 3 \right)!}}{(2x)^3}{(3y)^2}\\ = 10{(2x)^3}{(3y)^2}\\ = 720{x^3}{y^2}\end{array}\]

Middle Term of Binomial Expansion

The Middle Term of a Binomial Expansion is the term that comes in the middle of the expansion of the binomial, given by the Binomial Theorem. If the power of expansion of the sum or difference of two terms is an even number, then there is only one middle term. Otherwise, there are two middle terms.

How To Find Middle Term?

The middle term of a Binomial Expansion depends on the total number of terms in the given expansion. If n is even, (n+1) is odd so that the expansion will have an odd number of terms. In this case, the middle term is \[{(\dfrac{n}{2} + 1)^{th}}\] term. If n is odd, (n+1) will be even. So, there will be two middle terms, i.e., \[{(\dfrac{{n + 1}}{2})^{th}}\] term and \[{(\dfrac{{n + 1}}{2} + 1)^{th}}\]term. We will use the general term formula and put the value of r as \[{\textstyle{n \over 2}}\], if n is even to find the middle term. This is illustrated by the following diagram:

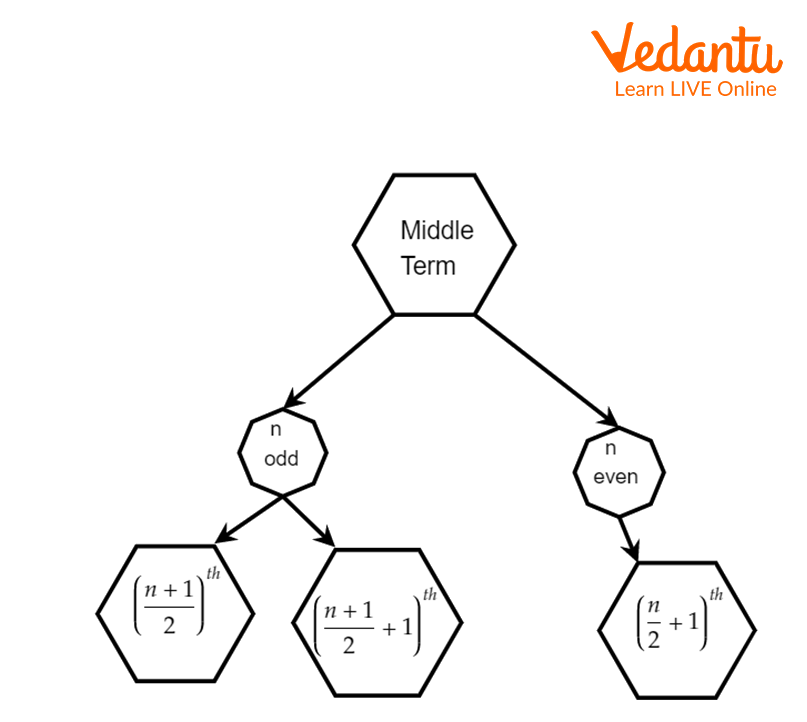
Middle Terms of a Binomial Expansion

Middle Term Example

Let us understand this by an example. Given a Binomial Expansion \[{(x + {\textstyle{1 \over x}})^4}\], n=4 which is even. So, n+1=4+1=5 is odd. So, the middle term is \[{(\dfrac{4}{2} + 1)^{th}} = {(2 + 1)^{th}} = {3^{rd}}\]term, which is

\[\begin{array}{l}{T_3} = {T_{2 + 1}} = {}^4{C_2}{(x)^{4 - 2}}{({\textstyle{1 \over x}})^2}\\ = \dfrac{{4!}}{{2!\left( {4 - 2} \right)!}}{x^2}.\dfrac{1}{{{x^2}}}\\ = 6\end{array}\]

For Binomial Expansion \[{(2x - y)^7}\], n=7, so, n+1=8 which is even. The middle terms are \[{(\dfrac{{7 + 1}}{2})^{th}} = {(\dfrac{8}{2})^{th}} = {4^{th}}\]and \[{(\dfrac{{7 + 1}}{2} + 1)^{th}} = {(\dfrac{8}{2} + 1)^{th}} = {(4 + 1)^{th}} = {5^{th}}\], i.e., \[\begin{array}{l}{T_4} = {T_{3 + 1}} = {}^7{C_3}{(2x)^{7 - 3}}{( - y)^3}\\ = \dfrac{{7!}}{{3!\left( {7 - 3} \right)!}}(2x)^4({-y^3})\\ =-560{x^4}{y^3}\end{array}\]

and \[\begin{array}{l}{T_5} = {T_{4 + 1}} = {}^7{C_4}{(2x)^{7 - 4}}{( - y)^4}\\ = \dfrac{{7!}}{{4!\left( {7 - 4} \right)!}}{(2x)^3}{y^4}\\ = 35(8{x^3}){y^4}\\ = 280{x^3}{y^4}\end{array}\]

Interesting Facts

• The Binomial Theorem is used in Probability and Statistics. Our economy depends on it.

• It is used for finding higher power roots of equations.

• It is used to predict the weather and for giving rank to candidates.

Solved Examples

1. Find the middle terms in the expansion of (3-x3)7.

Ans: Given Binomial Expansion is (3-x3)7.

Here, n=7. So, n+1=8, which is even. The middle terms are \[{(\dfrac{{7 + 1}}{2})^{th}} = {(\dfrac{8}{2})^{th}} = {4^{th}}\]and \[{(\dfrac{{7 + 1}}{2} + 1)^{th}} = {(\dfrac{8}{2} + 1)^{th}} = {(4 + 1)^{th}} = {5^{th}}\], i.e.,

\[\begin{array}{l}{T_4} = {T_{3 + 1}} = {}^7{C_3}{(3)^{7 - 3}}{( - {x^3})^3}\\ = \dfrac{{7!}}{{3!\left( {7 - 3} \right)!}}(3^4)( - {x^9})\\ = - 2835{x^9}\end{array}\]

and

\[\begin{array}{l}{T_5} = {T_{4 + 1}} = {}^7{C_4}{(3)^{7 - 4}}{( - {x^3})^4}\\ = \dfrac{{7!}}{{4!\left( {7 - 4} \right)!}}{(3)^3}{({x^3})^4}{( - 1)^4}\\ = 35(27)({x^{12}})(1)\\ = 945{x^{12}}\end{array}\]

The middle term are \[945{x^{12}}\]

2. Show that the Middle Term in the expansion of (1+x)2m is \[\dfrac{{1.3.5.7...(2m - 1)}}{{m!}}{2^m}{x^m}\] where m is a positive integer.

Ans: Given Binomial Expansion is (1+x)2m.

Step 1:

Finding the number of terms of the middle term:

Here, n=2m. So, n+1=2m+1, which is odd. So, the middle term is \[{(\dfrac{{2m}}{2} + 1)^{th}} = {(m + 1)^{th}}\]term.

The general term of \[(r+1)^{th}\] of \[(1+x)^n\] is \[{T_{r + 1}} = {}^n{C_r}{x^r}\]

Step 2:

Compute \[{(m + 1)^{th}}\]term of given expansion using the formula of general term:

\[{T_{m + 1}} = {}^{2m}{C_m}{(1)^{2m - m}}{(x)^m}\]

\[\begin{array}{l} = {}^{2m}{C_m}{(1)^{2m - m}}{x^m}\\ = \dfrac{{(2m)!}}{{m!\left( {2m - m} \right)!}}{(1)^m}{x^m}\end{array}\]

\[\begin{array}{l} = \dfrac{{(2m)(2m - 1)(2m - 2)...(m + 1)m(m - 1)...2.1}}{{m!m!}}(1){x^m}\\ = \dfrac{{(2m)(2m - 1)(2m - 2)...2.1}}{{m!m!}}{x^m}\end{array}\]

\[\begin{array}{l} = \dfrac{{\{ 2m(2m - 2)(2m - 4)...(2m - (2m - 2))\} \{ (2m - 1)(2m - 3)....(3)(1)\} }}{{m!m!}}{x^m}\\ = \dfrac{{\{ 1.3.5...(2m - 1)\} \{ m(m - 1)(m - 2)...3.2.1\} {2^m}{x^m}}}{{m!m!}}\\ = \dfrac{{m!\{ 1.3.5...(2m - 1)\} {2^m}{x^m}}}{{m!m!}}\\ = \dfrac{{1.3.5...(2m - 1){2^m}{x^m}}}{{m!}}\end{array}\]

3. Find the value of α for which the coefficients of middle terms in the expansion of (1+αx)4 and (1-αx)6 are equal.

Ans: Consider the expression (1+αx)4. Here, n=4. So, n+1=4+1=5, and 5 is odd. The middle term is \[{(\dfrac{4}{2} + 1)^{th}} = {(2 + 1)^{th}} = {3^{rd}}\]term.

Now, T3=T2+1

\[\begin{array}{l} = {}^4{C_2}{(1)^{4 - 2}}{(\alpha x)^2}\\ = \dfrac{{4!}}{{2!\left( {4 - 2} \right)!}}{(1)^2}{\alpha ^2}{x^2}\\ = 6{\alpha ^2}{x^2}\end{array}\]

Now, consider the expression (1-αx)6. Here, n=6. So, n+1=6+1=7, and 7 is odd. The middle term is \[{(\dfrac{6}{2} + 1)^{th}} = {(3 + 1)^{th}} = {4^{th}}\]term.

T4=T3+1

\[\begin{array}{l} = {}^6{C_3}{(1)^{6 - 3}}{( - \alpha x)^3}\\ = \dfrac{{6!}}{{3!\left( {6 - 3} \right)!}}{(1)^3}( - {\alpha ^3}{x^3})\\ = - 20{\alpha ^3}{x^3}\end{array}\]

Since the coefficients of both the middle terms are equal, so comparing both, we get

6α2 = -20α3

\[\begin{array}{l} \Rightarrow - \dfrac{6}{{20}} = \dfrac{{{\alpha ^3}}}{{{\alpha ^2}}}\\ \Rightarrow - \dfrac{3}{{10}} = \alpha \\ \Rightarrow \alpha = - \dfrac{3}{{10}}\end{array}\]

The value of α for which the coefficients of both the middle terms are equal is \[( - \dfrac{3}{{10}})\].

Key Features

• The position of the middle term of a binomial expansion depends on the total number of terms contained in the expansion(n+1).

• If n is odd, the Binomial Expansion will have two middle terms: \[{(\dfrac{{n + 1}}{2})^{th}}\] and \[{(\dfrac{{n + 1}}{2} + 1)^{th}}\].

• If n is even, the Binomial Expansion will have one middle term: \[{(\dfrac{n}{2} + 1)^{th}}\] .

Practice Questions

1. Find the middle terms in the expansion of

1. \[\left ( \dfrac{2x}{3} - \dfrac{3}{2x} \right )^{20}\]

2. \[\mathrm {(1-2x+x^2)}^{10}\]

2. Prove that the coefficient of the middle term in the expansion of \[{(1+x)}^{2n}\] is equal to the sum of coefficients of the middle terms of the expansion \[{(1+x)}^{2n-1}\].