The term in the nth position from the first (left side) of an arithmetic progression is known as the $n^{th}$ term of AP. An arithmetic progression is a sequence where the differences between two subsequent terms are the same.

$n^{th}$ Term Formula:

Suppose that an equation reference goes here. $a_{1}, a_{2}, a_{3},...$be an arithmetic progression (AP), in which the first term $a_1$ is equal to “a” and the common difference is taken as "d.", then the second term, third term and so on can be determined as shown below:

Second term,

\[{{a}_{2}}~=\text{ }a+d\]

Third term, \[{{a}_{3}}~=\text{ }\left( a+d \right)+d\text{ }=\text{ }a+2d,\]

Fourth term, \[{{a}_{4}}~=\text{ }\left( a+2d \right)+d\text{ }=\text{ }a+3d\], and so on.

As a result, the nth term of an AP ($a_n$) with the first term “a” and common difference “d” is given by the formula:

$n^{th}$ term of an AP, \[{{a}_{n}}~=\text{ }a+\left( n-1 \right)d.\]

$n^{th}$ term of AP

General term of AP:

Formula for the nth term of the A.P. with first term ‘a’ and common difference ‘d’ is ${{a}_{n}}=\text{ }a\text{ }+\text{ }\left( n-1 \right)\text{ }d. n^{th}$ term (${{a}_{n}}$) is also termed as the general term of the AP.

As a result , the General Term of an $a_{n}=a+(n-1)d$. If there are ‘\[n\]’ terms in the AP, then \[{{a}_{n}}\] symbolizes the last term which is sometimes also indicated by ‘\[l\]’.

Sum of n Terms in an A.P:

A Math lesson for grade \[10\] was held in Germany in the nineteenth century. The teacher instructed her students to add all of the numbers from \[1to100\]. The students were having difficulty calculating the sum of all these numbers. While the other pupils were still calculating the amount, one youngster screamed out the answer \[5050\]. Carl Friedrich Gauss, the brilliant German mathematician, was this youngster. How did he come up with the figure so quickly?

He noticed that terms equidistant from the start and end of the series had a constant sum of \[101\].

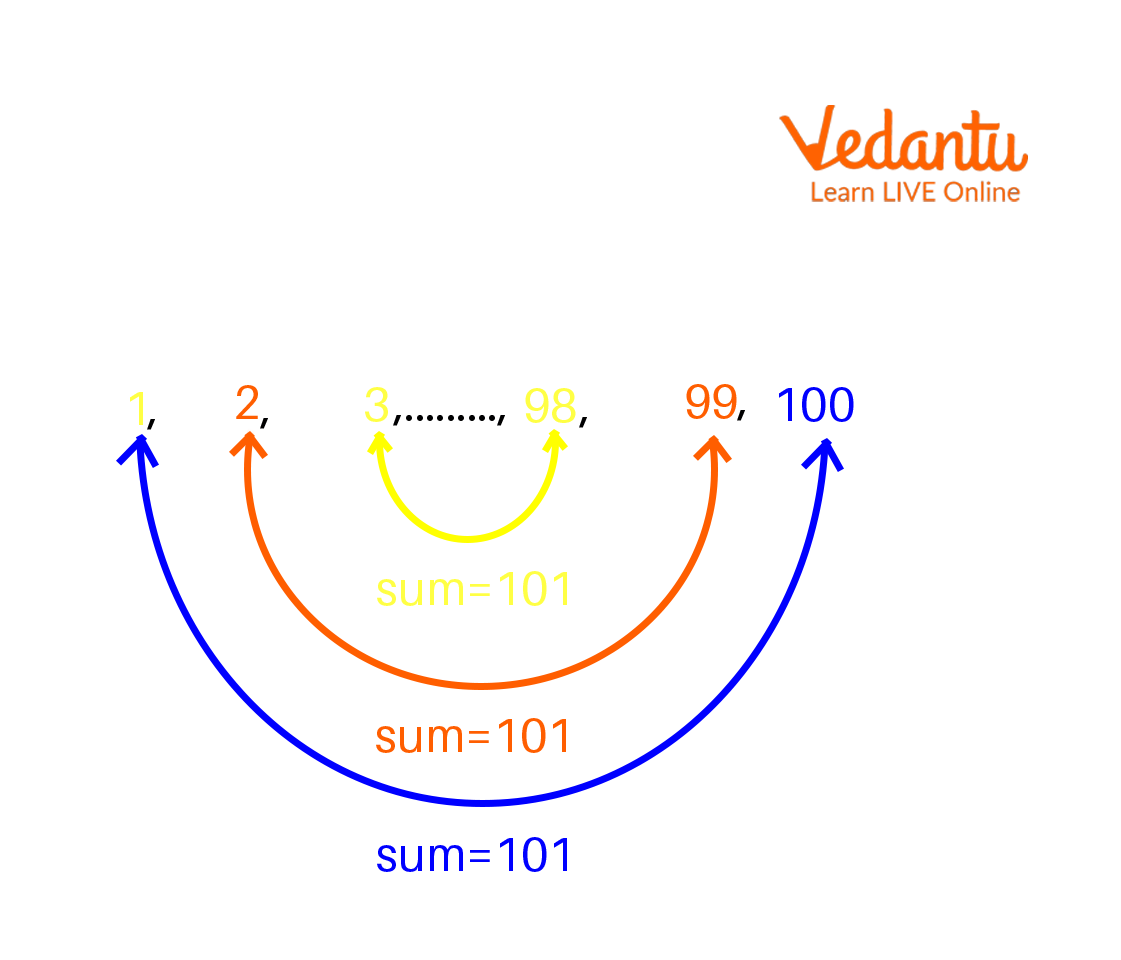
Constant Sum of the series

We can recognize that there are \[50\]such pairs whose sum is \[101\] in the series \[1,\text{ }2,\text{ }3,...,\text{ }100.\] As a result, the sum of all terms in this series is \[50\times 101\] =\[5050\].

Sum of n Terms of AP Formula:

The sum of n terms of an AP can be simply calculated using a simple formula that states that if the first term of the AP is a and the common difference is d, the formula for the sum of n terms of the AP is

\[{{S}_{n}}=\text{ }\dfrac{n}{2}\left[ 2a\text{ }+\text{ }\left( n-1 \right)d \right]\]

Example: Calculate the sum of the first 20 terms of the following AP: $S=190+167+144+121+...$

Solution: Using the sum of n terms of an AP formula,

\[{{S}_{n}}=\text{ }\dfrac{n}{2}\left[ 2a\text{ }+\text{ }\left( n-1 \right)d \right]\]

Here, we have \[a\text{ }=\text{ }190,\text{ }d\text{ }=\text{ }-23,\text{ }and\text{ }n\text{ }=\text{ }20\]. Putting all these values in the above formula,

$S=\dfrac{20}{2}(2(190)+(20-1)(-23))$

$=10(380-437)$

$10(-57)$

$-570$

As a result, the sum of the first 20 terms of the given AP is -570.

How to Find the nth Term in AP?

Procedure for determining the nth term:

Step 1: First, find the first and second terms, $a_{1}$ and $a_{2}$

Step 2: Next, calculate the common difference between them, which is $[d=a_{2}-a_{1}]$.

Step 3: Now, by adding the difference d to the second term, we get the third term, and so on. That is the second term, $a_2=a_1+d$ ($a_1$ is first term)

$a_3=a_2+d=\left( a_1+d \right)+d=a_1+2d$ is the third term.

$a_4=a_3+d=\left( a_1+2d \right)+d=a_1+3d$ is the fourth term.

As a result, the coefficient of d is one less than the number of words. That is to say,

The coefficient of d in $a_2$ is 1 $\left[ \left( 2-1 \right)=1 \right]$.

The coefficient of d in $a_3$ is 2, $\left[ \left( 3-1 \right)=2 \right]$.

The coefficient of d in $a_4$ is 3, $\left[ \left( 4-1 \right)=3 \right]$.

Likewise, the number of d for the $N^{th}$ term should be $\left( N-1 \right)$ times.

As a result, $a = a_1 + \left( N-1 \right)d \left[ \text{First term}+ \left( \text{Last term}-1 \right)\text{common difference} \right]$.

Example : Determine the 9th term of the following series: \[1,\text{ }4,\text{ }7,\text{ }10,\text{ }13,\text{ }16,....\]

Solution:

Here,first term,$a_1 = 1$, second term, $a_2 = 4$, third term, $a_3 = 7$, forth term, $a_4=10$.

$d=a_2 - a_1 = 4 - 1=3$ is the common difference.

Check if d is true or not.

$a_1+ d = 1+3 =4 =a_2$

$a_2+d = 4+3=7=a_3$

$a_3+d=7+3=10=a_4$

$a_4+d=10+3=13=a_5$

$a_5+d=13+3 =16=a_6 $

So the common difference is right here.

Now the $9^{th}$ term,

$a_9=a_1+\left( N-1 \right)d$

$=1+\left( 9-1 \right) \times 3$

$ =1+8 \times 3$

$=1+24$

$=25$

As a result, the $9^{th}$ term is 25.

How Do You Determine the Number of Terms in an Arithmetic Sequence?

Calculating the number of terms in an arithmetic sequence may appear to be a difficult problem, but it is quite simple. Simply enter the above numbers into the formula \[{{t}_{n}}=\text{ }a\text{ }+\text{ }\left( n\text{ }-\text{ }1 \right)\]d and solve for n, the number of terms. It's worth noting that tn is the last number in the sequence, a is the first term, and d is a common difference.

Tips: The common difference will always divide the difference between the last and first terms.

Solved Questions:

Q.1: An AP's third term is 5 and its seventh term is 9. Determine the arithmetic progression (AP).

Solution: As a result, the third term of AP = 5.

AP's seventh term = 9

$\left( i.e \right) a_3 = a+\left( 3-1 \right)~ $

$d = a+2d = 5 \ldots \left( 1 \right)~ $

$a_7 =a+\left( 7-1 \right)~ $

$d= a+6d = 9 \ldots \left( 2 \right)~ $

When we solve equations $\left( 1 \right)$ and $\left( 2 \right)$, we get

a=3 and d = 1.

As a result, the first term is 3, and the common difference is 1.

The arithmetic progression $\left( AP \right)$ is thus $3, 4, 5, 6, 7, 8, 9,...$

Q.2: Given \[a\text{ }=\text{ }5,\text{ }d\text{ }=\text{ }3,\text{ }and\text{ }{{a}_{n}}~=\text{ }50\], find the value of \[{{S}_{n}}\].

Solution: The given values are $a =5=a_{1}, d=3$, and ${{a}_{n}}=50$.

We know that the $n^{th}$ term of AP is given by the formula ${{a}_{n}}=a+\left( n-1 \right)d$.

$\Rightarrow 50=5+\left( n-1 \right)3 $

$50=5+3n-3$

$50=3n+2$

$48=3n$

$16=n$

By using the sum of AP formula,

${{S}_{n}}~=\dfrac{n}{2}\left( {{a}_{1}}+{{a}_{n}} \right)$

${{S}_{n}}~=\dfrac{16}{2}\left( 5+50 \right)$

${{S}_{n}}~=8\left( 55 \right)$

${{S}_{n}}~=440 $

Thus, the value of $S_{n}$ is 440.

Q.3 Find the value of m if the total of an A.P.'s “n” terms is $3n^{2}+5n$ and its $m^{th}$ term is 164.

Solution: Let $S_n$​ denote the sum of n terms and $a_n$​ be the $n^{th}$ term of the given AP. Then,

$S_{n}=3n^{2}+5n$

$S_{n-1}=3(n-1)^{2}+5(n-1)=3n^{2}-n-2$

Now,$a_{n}=S_{n}-S_{n-1}$

$a_{n}=3n^{2}+5n-3n^{2}+n+2$

$a_{n}=6n+2$

Now, $a_m=164$

$6m+2=164$

$6m=162$

$m=27$

Related Articles:

• Arithmetic Progression

• Sequence and Series

Conclusion:

• The common difference does not always have to be positive.

• An AP's common difference is the difference between any term and its prior term, in this order.

• The first term of AP can be calculated using the formula a = \[T_{n}\text{ }-\text{ }\left( n\text{ }-\text{ }1 \right)d.\]