Properties of a Parallelogram: A Brief Introduction
In two dimensions, a parallelogram is a geometric shape with parallel sides. It has two parallel sides that are of the same length, making it a four-sided polygon (sometimes referred to as a quadrilateral). The sum of the adjacent angles of a parallelogram is 180 degrees.
Parallelograms are a unique class of polygons. It is a quadrilateral in which the opposite sides of both pairs are parallel. A parallelogram's characteristics make it simple and quick to distinguish between several given shapes.
The word "parallelogram," which means "bounded by parallel lines," is derived from the Greek word "parallelogramma". Let's find out more about parallelograms, their characteristics, and some examples.
Concept of a Parallelogram
Having two sets of parallel sides makes a quadrilateral a parallelogram.
A parallelogram has opposite sides that are the same length and angles that are of the same measure.
Additionally, the internal angles on the transverse side are supplementary. The total internal angles add up to $360^\circ $.
A parallelepiped is a three-dimensional shape with faces that are parallelograms.
The area of a parallelogram is given by its base, which is one of its parallel sides, and height, which is the difference between its top and bottom heights. The lengths of a parallelogram's four sides determine the perimeter of that parallelogram.
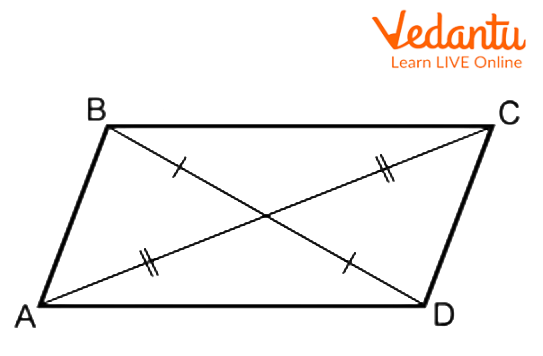
Parallelogram ABCD with Equal Diagonals
As you can see from the previous figure, ABCD is a parallelogram where $AB\parallel CD$ and $AD\parallel BC$.
Furthermore, $AB = CD$ and $AD = BC$ .
In addition, $\angle A = \angle C$ & $\angle B = \angle D$ .
$\angle A$ and $\angle D$ are supplementary angles as well because they are located on the same side of the transversal. The additional angles $\angle B$ and $\angle C$ function similarly.
Consequently, $\angle A + \angle D = 180^\circ $, $\angle B + \angle C = 180^\circ $.
Shape of a Parallelogram
A parallelogram has two dimensions. Each of its four sides has two parallel pairs of sides. Additionally, the parallel sides have the same length. If the parallel sides are not equal, the shape is not a parallelogram. Similarly to this, a parallelogram must always have equal inner angles on both sides. Otherwise, the given shape will not be a parallelogram.
Some Special Types of Parallelograms
Square and Rectangle: Two forms that resemble a parallelogram in terms of its characteristics are the square and the rectangle. Both have their opposing sides parallel to and equal to one another. Both squares and rectangles have diagonals that bisect each other in two equal halves.
Rhombus: If all of a parallelogram's sides are congruent or equal to one another, the parallelogram is a rhombus.
Rhomboid: This is a unique type of parallelogram with opposite sides that are parallel to one another but the neighbouring sides are of different lengths. The angles are also all 90 degrees.
Trapezium: If there are two parallel sides and two non-parallel sides, the shape will be a trapezium.
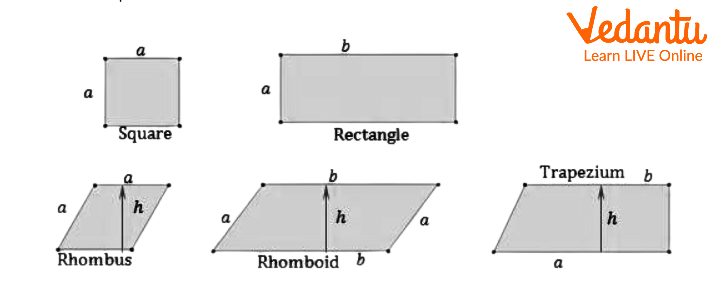
Different Types of Parallelograms
What Are the Properties of a Parallelogram?
A quadrilateral is a special type of polygon, which can be known as a parallelogram if it contains two parallel opposite sides. A parallelogram has the following properties:
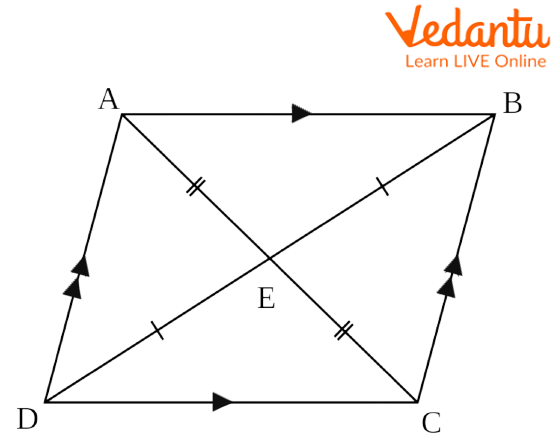
Properties of a Parallelogram
The opposing sides are congruent and parallel. Segment AB is parallel and congruent to segment DC, while segment AD is parallel and congruent to segment BC.
The opposing angles show congruency. Angle A is congruent with angle C, while angle D is congruent with angle B.
Consecutive interior angles on the same side have a supplementary sum. Angles A and D are supplementary, as angles B and C. Similarly, angles A and B, angles D and C.
All of the angles will be at right angles if any one of them is a right angle.
Each of the two diagonals intersects the other diagonal.
A parallelogram can be divided into two congruent triangles by each of its diagonals. Triangle DCB and triangle DAB are congruent.
Formulas for Area and Perimeter of a Parallelogram
The next section discusses the formula for a parallelogram's area and perimeter. These equations can be used by students to solve difficulties.
Parallelogram's Area
A parallelogram's area is the area that it takes up in a two-dimensional plane. The formula to calculate the parallelogram area is listed below:
Base x Height = Area
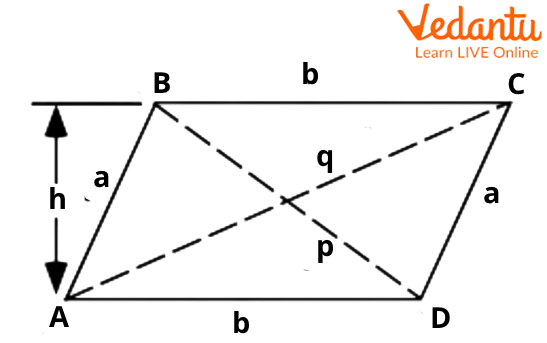
Parallelogram
Parallelogram's Perimeter
The sum of the distances between the parallelogram's boundaries equals its perimeter. We must be aware of the length and width measurements in order to determine the perimeter value. The parallelogram's opposing sides are of equal length. In order to compute the perimeter, the following formula is used:
Perimeter $ = 2(a + b)$ units.
where the parallelogram's side lengths are $a$ and $b$.
Solved Examples
Q.1. The quadrilateral ABCD has an AB value of $8.5$ units. ABCD's diagonals are right angles to one another. Determine ABCD's perimeter.
Solution. A quadrilateral is a rhombus if its diagonals intersect at right angles, as determined by the characteristics of parallelograms.
Therefore, ABCD is a rhombus, and $AB = BC = CD = DA$ follows.
The perimeter then equals $4 \times AB = 4 \times 8.5 = 34$ units.
Q.2. Determine the area of a parallelogram with a $5$cm base and an $8$ cm height.
Solution. The base is $5$ cm, and the height is $8$ cm.
Knowing that Area = Base x Height
Area $ = 5 \times 8$
Area $ = 40$sq. cm
So, the area is $40$sq.cm
Practice Questions
A parallelogram with sides of $20$ and $15$ metres has a diagonal of length $15$ metres. What is the area of such a parallelogram?
Find the area of a parallelogram whose adjacent sides are $15$ cm and $8$ cm.
Answers
$100\sqrt 5 $ sq. m
$46$ sq. cm
Summary
The learning outcomes from the parallelogram topic will help in properly understanding all the geometric shapes related to a parallelogram, how to determine a parallelogram's area and perimeter, and examples of where we might see a parallelogram in daily life. In this article, we have undertaken an in-depth study of the geometrical figure, parallelogram and also discussed its properties. Do try to solve the examples and practice questions provided above to enhance your understanding of the topic further.
List of Related Articles
FAQs on Parallelogram
1. What are the Important Formulas of Parallelogram Kite, and Trapezium Which is Mostly Used?
Some important formulas of Trapezium, Kite, and Parallelogram are given below.
The area of a parallelogram is the area occupied by it in a two-dimensional plane.
Area of a parallelogram = Base × Height
The perimeter of a parallelogram is the measurement is the total distance of the boundaries of a parallelogram.
Perimeter of a parallelogram = 2(a+b)
Here, a and b are the length of the equal sides of the parallelogram.
The area of the trapezium can be calculated by taking the average of the two bases of a trapezium and multiplying by its altitude.
Area of a trapezium A, = h(a+b)/2
Where,
h is the height of the trapezium and a,b are the bases of a trapezium.
Perimeter of a Trapezium -
The perimeter of a trapezium is calculated by adding all its sides. Hence, the formula of the perimeter of a trapezium is given by
Perimeter of a trapezium = a + b +c+ d
Here, a,b,c and d are the sides of the trapezium.
A kite has two pairs of each side. The total distance around the outside of a kite is known as the perimeter of a kite. The perimeter of a kite is calculated by finding out the sum of the length of each pair of the equal sides of a kite.
Perimeter of a Kite = 2a +2b
Here,
a and b are the length of the first and second pair of the sides of a kite.
Area of a Kite
As we know diagonals of a kite are perpendicular. Accordingly, the area of a kite is expressed as half of the product of its diagonals which is similar to that of a rhombus.
Area of a Kite = ½ d₁d₂
d₁ - Long pair of diagonal
d₂ - Short pair of diagonal
2. Is Square and Rectangle Considered as a Parallelogram?
The geometrical figures such as square and rectangle are both considered as parallelograms as the opposite sides of the square are parallel to each other and the diagonals of the square bisect each other. The rectangle is a special case of a parallelogram in which measures of its every interior angle is 90 degree. It is also known as an equiangular quadrilateral.
Rectangle also have similar properties of parallelograms such as the opposite sides of a rectangle are parallel to each other as parallelogram.
3. What parallelogram properties can we use to distinguish between a parallelogram and a quadrilateral?
A parallelogram-shaped object always has opposite sides that are the same length. Sometimes the opposite sides of a quadrilateral form do not have sets of opposite sides that have the same length. Every quadrilateral can be referred to as a parallelogram, but not every parallelogram can be referred to as a quadrilateral. While a kite and a trapezium are both considered quadrilaterals, they fall short of meeting all of the requirements of a parallelogram and cannot be referred to as such.
4. What are the distinctive characteristics of each unique parallelogram?
It is true that not all quadrilaterals are made equal; parallelograms are a good example of this. The parallelograms square, rectangle, and rhombus are three of their specific varieties. A four-sided polygon with a square shape is one with equal sides and angles. In a rectangle, the opposing sides are parallel and equal. Rectangles and squares have equal, $90^\circ $ angles at every intersection. Although a rhombus is a parallelogram with four equal sides, its angles are not required to be right angles.
