The Prime Factors of 25
A prime number can only be divided by itself and one without leaving any remains. Whenever you divide a prime number by another natural number, you get numbers left over. Every other natural number is made up of prime number factors. Simply put, a number’s prime factors are the prime numbers that are multiplied to generate the original number. For example, the prime factors of 25 are 5 and 5, i.e, $5 \times 5=25$. This article will help you understand the concepts of prime factors in general.
What is Prime Factorization?
Prime factorization is simply a process in which a number is broken down into prime numbers that help construct the number when multiplied. In other words, prime numbers are multiplied together to get the original number. Here are some prime factorization examples:
8 = $2 \times 2 \times 2=2^{3}$
18 = $2 \times 3 \times 3=2 \times 3^{2}$
25 = $5 \times 5=5^{2}$
20 = $2 \times 2 \times 5=2^{2} \times 5$
Methods for Prime Factorization
There are several methods for prime factoring an integer. The most frequent methods for prime factorization are:
Factor tree method
Division method
Factor Tree Method
This method places the given number on top of the factor tree. The relevant pairs of factors are then written as the tree's branches. Following this, the composite factors are factored in and written down as the next branches.
The following steps are used to find out what are the prime factors of a 25 using the factor tree method:
First, above the factor tree, put the number 25.
Then, write down the relevant pair of factors in tree branches.
Factorise the composite factors discovered in step 2 and record the pair of factors as the tree's next branches.
Repetition of step 3 is required to obtain the prime factors for each composite factor.
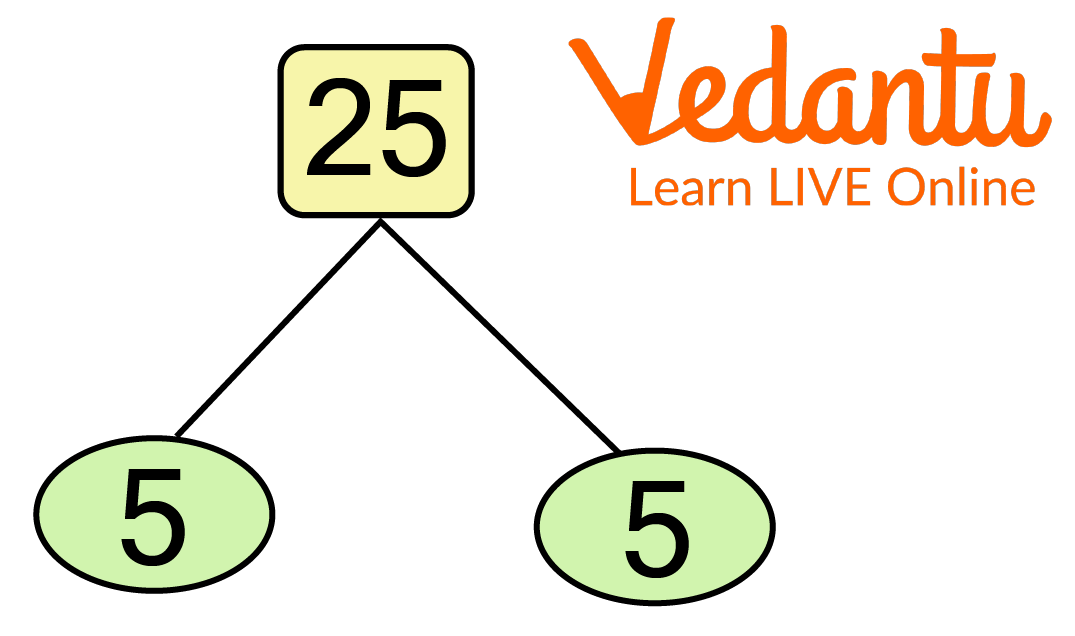
Prime Factorization of 25 Using Tree Method
Division Method
In this method, the given integer is divided by the smallest prime number that entirely divides it. The quotient is then divided by the smallest prime integer once more. This process is repeated until the quotient equals one.
The following steps are used to find out the prime factors of 25 using the division method:
Divide 25 by the lowest prime number, in this case, 5, ensuring that the smallest prime number entirely divides the number.
Divide the quotient of step 1 (5) by the smallest prime integer (5) once more.
Repeat step 2 until the quotient equals one.
Finally, multiply all of the divisors' prime factors to get the products of the prime factors of 25.
Prime Factorization of 25 Using Division Method
Solved Examples
1. Find the prime factors of 64.
Ans: Prime factors of 64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
2. Find the prime factors for 1620.
Ans: To find the factors of 1620, you can use the factor tree method. The prime factorization of 1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5.
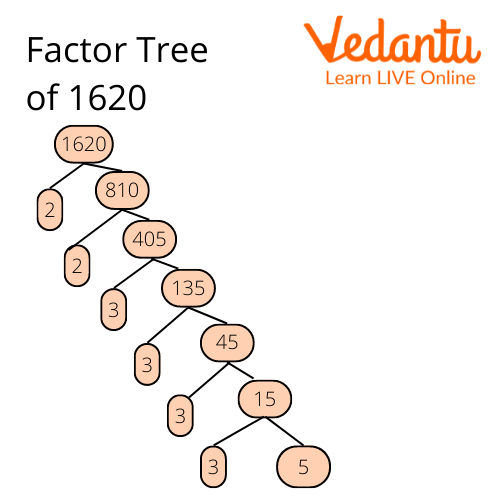
Prime Factorization of 1620 Using Tree Method.
3. Find the prime factors of 7429.
Ans: We can find the prime factors of 7429 by either factor tree or divisional method.
Using the divisional method, we can get prime factors 17 x 19 x 23.
Prime Factorization of 7429 Using Tree Method
Practice Questions
1. Find the Prime Factor of 544 using the factorial tree method.
Ans: The prime factorization of 544 is 2×2×2×2×2×17 or 24 x 17.
2. Find the prime factors of 1000.
Ans: The prime factorization of 1000 is 2 x 2 x 2 x 5 x 5 x 5 or 23 x 53.
3. Find the prime numbers of 45.
Ans: The prime factorization of 45 is 3 × 3 × 5 or 32 × 5.
4. Find the prime numbers of 88.
Ans: The prime factors of 88 are 2 and 11.
5. Find the prime numbers of 50.
Ans: The prime factors of 50 are 2 × 5 × 5 or 2 × 52
Summary
As we have discussed earlier, Prime factorization is the process of breaking down a number into prime numbers that help construct the number when multiplied. There are two ways for prime factorization of any number. In the method of division, the given integer is divided by the smallest prime number that entirely divides it until the quotient equals one. The prime factors that are divisors are then multiplied. In the Method of the factor tree, the given number is placed on top of the factor tree. The relevant pairs of factors are then written as the tree's branches. Following this, the composite factors are factored in and written down as the next branches until all of the composite factors' prime factors are obtained.
FAQs on Prime Factorisation
1. Where do prime numbers and prime factorization come into play in everyday life?
Prime numbers have a wide range of applications. They are used by cicadas to determine the timing of their life cycles, by manufacturers to eliminate harmonics from their products, and by current screens to specify the colour intensities of their pixels.
Following are the famous applications of prime numbers and prime factorization
Prime numbers protect your funds.
Primes are used in the natural world
Prime numbers are used in Candy Crush.
Prime numbers are used nearly everywhere.
2. What is the purpose of prime factorization?
Any number can be represented as a sum of prime numbers by prime factorization. A number with exactly two factors, 1 and the number itself, is said to be a prime number. When dealing with whole numbers, prime factorization is a very helpful technique that is utilised in mental arithmetic, fractions, finding square roots, and computing the HCF and LCM of two smaller integers. Prime factorization is utilised to determine the greatest common factor of a given group of numbers. It is used to get the greatest common factor of 2 or more numbers in an easy manner.
3. How many different prime factorizations exist?
To "break down" or express a given number as a product of prime numbers, one uses the prime factorization technique. Furthermore, a prime number is typically represented in exponential form to make it appear more compact when it appears more than once in the factorization. Prime factorization can be done in one of two methods. The Prime Factor Tree is the first, while the Upside-Down Division is the second. One of two approaches can be used to prime factorise. The first is the Prime Factor Tree, while the second is the Upside-Down Division. Both are simple to use and can be applied in various numbers.