How to Apply the Pythagorean Theorem in Everyday Maths
The Greek philosopher Pythagoras is credited with discovering a crucial and practical characteristic of right-angled triangles. Thus, the property bears his name. Whether you have to measure the steepness of the mountains or the shortest path between two places, Pythagoras theorem has great use. It says when you add a square of legs the right angle triangle is equal to a square of the hypotenuse.
What is a Right-angle Triangle?
The right angle triangle is a triangle whose one of interior angle is 90. Since 90 is also known as the right angle so we call this triangle a right-angle triangle. At a right angle, triangle sides got special names. The side which is just opposite the right angle is known as hypotenuse and the other two sides are called the legs of that triangle. The right triangles are categorized as isosceles right triangles and scalene right triangles based on the different sides' values.
In the following figure triangle, ABC is the right angle triangle where AB is perpendicular/altitude and BC is the base and the longest side opposite to the correct angle is the Hypotenuse.
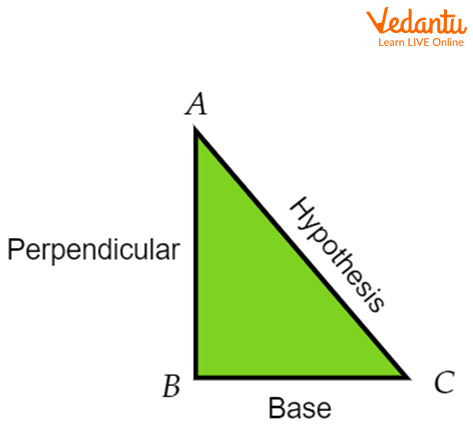
A Right-angled Triangle
Area of a Right-angle Triangle
The portion covered inside the triangle's perimeter is referred to as the right triangle's area. The sides of a right-angle triangle are knowns as height, base, and hypotenuse. The terms base and height can be used interchangeably to refer to the two legs. The formula for the area of a right-angle triangle is -
Area of right angle triangle = \[\dfrac{1}{2}\times \text{base}\times\text{height}\]
What is Pythagoras Theorem?
Pythagoras is a powerful theorem that establishes the relation among sides of a right-angle triangle. According to Pythagoras theorem -
“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”. Mathematically we can write it as
\[\text{hypotenuse}^2=\text{Perpendicular}^{2}+\text{Base}^{2}\]
The above-mentioned formula is known as Pythagoras theorem formula or right angle triangle formula.
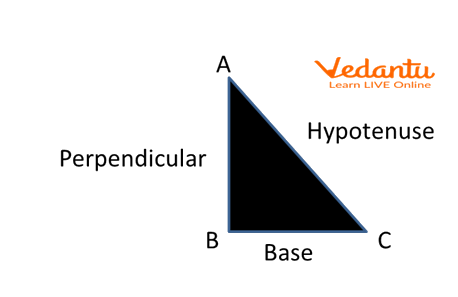
A Right-angled Triangle Demonstrating Pythagoras Theorem
Proof of Pythagoras Theorem
Graphical proof of Pythagoras theorem requires some construction as follows-
Steps 1- Prepare 8 right-angled triangles identical to each other. Keep hypotenuse as c unit and other sides as a unit of base and b unit of perpendicular.
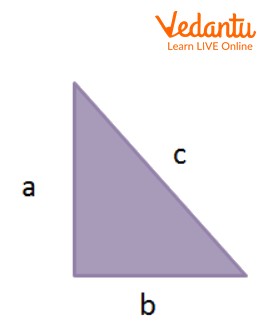
Right Angle Triangle That We Have to Draw 8 Times
Steps 2- Now construct two squares of side a+b.
Step 3- Now put four triangles in the first square and the rest four in the other square as per shown in the figure below.
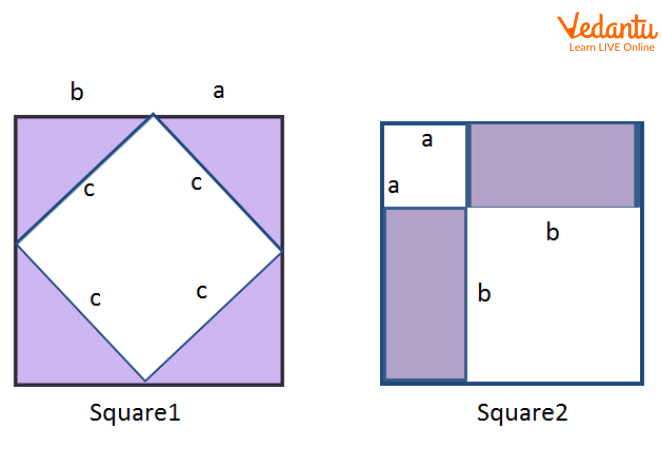
Two Identical Squares of Side a+ b
Observing both identical squares containing 4 triangles each are also identical, one can infer that-
The uncovered area of square1 is equal to the uncovered area of square2
Therefore-
\[c^{2}=a^{2}+b^{2}\]
This is the Pythagoras theorem i.e. the sum of the square of right angle triangle = square of the hypotenuse.
Pythagoras Triplet
Pythagoras triplet is a group of three positive integers such that they follow the rule given below-
\[a^{2}+b^{2}=c^{2}\]
Pythagoras triplets are denoted as (a,b,c) . for example- (20,21,29)
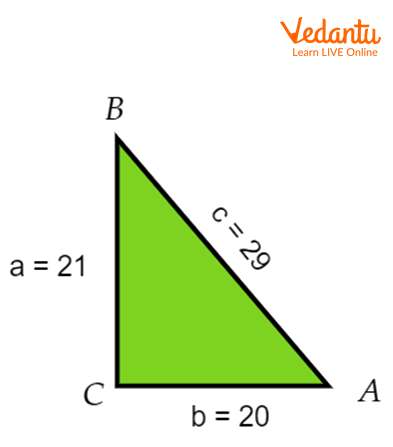
Demonstration of Pythagoras Triplet
Application of Pythagoras Theorem
We can use Pythagoras theorem as follows-
If two sides of the right angle are known we can find another side
We can check whether the right-angle triangle is possible or not from the given value of sides.
Interesting facts
If a triangle is following Pythagoras theorem then it must be a right triangle.
A straight line connecting the center point of the hypotenuse of a right-angled triangle to the right angle equals half the hypotenuse.
In a triangle, the longest side is the one that forms the greatest angle.
Solved Problems
Q1. Which of the following is Pythagoras triplet?
a) (3,4,5) b) (5,6,7)
Ans - a) \[5^{2}=25\] and \[3^{2}+4^{2}=25\]
So \[5^{2}=3^{2}+4^{2}\]
Hence it is Pythagoras triplet.
b) \[7^{2}=49\] and \[5^{2}+6^{2}=61\]
Hence (5,6,7) is not Pythagoras triplet.
Q2. We are given sides of triangles as (5cm, 12 cm, and 13cm). Find if this triangle is a right-angle triangle or not.
Ans- 13cm is the longest side so it is the hypotenuse and the rest are legs.
To be a right-angle triangle, it must follow Pythagoras theorem.
$13^2=169$ and $12^2+5^2=169$
Since this follows Pythagoras theorem hence this is a right-angle triangle.
Key Features
According to Pythagoras theorem -“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”.
The right angle triangle is a triangle whose one of interior angle is 90.
Area of right angle triangle = \[\dfrac{1}{2}\times \text{base}\times\text{height}\]
Pythagoras triplet is a group of three positive integers such that they follow the rule given below- \[a^{2}+b^{2}=c^{2}\]
Practice Questions
Que- Find the area of the following triangle.
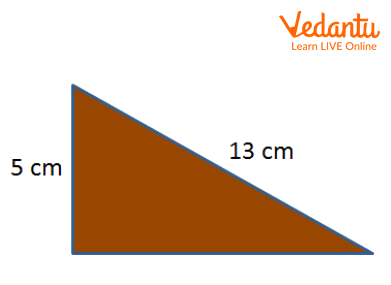
Practice Problem Figure 1
Ans - The answer is 30 \[\text{cm}^2\].
FAQs on Pythagorean Theorem Explained for Students
1. What is the Pythagorean theorem?
The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (legs). This fundamental relationship is a cornerstone of geometry.
2. What is the formula for the Pythagorean theorem?
The formula for the Pythagorean theorem is expressed as a² + b² = c². In this formula:
- a and b represent the lengths of the two legs (the sides that form the right angle).
- c represents the length of the hypotenuse.
3. Can you provide a real-world example of the Pythagorean theorem?
Yes. A common real-world example is in construction. If a carpenter needs to ensure a corner is a perfect 90-degree angle, they can measure 3 units along one wall and 4 units along the other. If the distance between those two points is exactly 5 units, the corner is a right angle because 3² + 4² = 9 + 16 = 25, which is 5². This application is often called the 3-4-5 rule.
4. How is the proof of the Pythagorean theorem demonstrated in the CBSE syllabus?
There are many ways to prove the Pythagorean theorem. A common visual proof, often taught as per the CBSE 2025-26 syllabus, involves arranging four identical right-angled triangles to form a large square with a smaller, tilted square in its center. By calculating the total area in two different ways (as one large square vs. the sum of the four triangles and the inner square), we can algebraically derive that a² + b² = c².
5. What is the difference between the Pythagorean theorem and its converse?
The main difference lies in their application and what they prove:
- The Pythagorean Theorem starts with a known right-angled triangle and helps you find the length of a missing side.
- The Converse of the Pythagorean Theorem starts with a triangle where all three side lengths are known. It helps you determine if the triangle is a right-angled triangle. If the side lengths satisfy the equation a² + b² = c², then the triangle must have a right angle.
6. What are Pythagorean triples and why are they important?
Pythagorean triples are sets of three positive integers (a, b, c) that perfectly satisfy the Pythagorean formula, a² + b² = c². The most famous example is (3, 4, 5). Other examples include (5, 12, 13) and (8, 15, 17). They are important because they provide a quick way to create or identify right-angled triangles with whole number side lengths, which is very useful in solving geometry problems and in exams.
7. Is the Pythagorean theorem applicable to all types of triangles?
No, the Pythagorean theorem is exclusively applicable to right-angled triangles. It does not hold true for acute triangles (where all angles are less than 90°) or obtuse triangles (where one angle is greater than 90°). Applying it to other triangle types will lead to incorrect calculations.
8. How can the Pythagorean theorem be used to find the length of a diagonal in a square or rectangle?
In a square or rectangle, the diagonal divides the shape into two identical right-angled triangles. The sides of the rectangle (length and width) act as the legs (a and b) of these triangles, and the diagonal itself becomes the hypotenuse (c). Therefore, you can calculate the diagonal's length using the formula: (diagonal)² = (length)² + (width)².
9. Who is credited with discovering the Pythagorean theorem?
While the theorem is named after the Greek mathematician Pythagoras (c. 570–495 BC), who is credited with its first formal proof, historical evidence suggests the relationship was known earlier. Civilizations in Babylon, Egypt, and India used this principle for construction and astronomy centuries before Pythagoras. However, Pythagoras' school is celebrated for formalizing it within a deductive mathematical framework.
