What Is the Reflection in Y Axis Formula and Rule
Have you ever thought about how you would represent the reflection of a point in the y-axis? This is accomplished through the use of reflection in the y-axis concept. If you do not know about it, do not get worried, as this article covers all the concepts of reflection in the y-axis, and the graph xy = 1 is reflected in y = 2x using attractive images so that the children can easily grasp the topics. Let us now begin our learning.
What is the Reflection of a Point in the y-axis?
Reflection of a point in the y-axis states that the y-coordinate stays the same when a point is reflected across the y-axis, the x-coordinate is assumed to be the additive inverse of the given abscissa. For example, a point (x, y) is reflected across the y-axis as (-x, y).
Reflection of a point in the y-axis
A Point on the y-axis has Coordinates
A point on the y-axis has coordinates in the form of ordered pairs having the form (0, k), where k is the point on the y-axis. Here, 0 specifies the distance between the abscissa and the origin. When x = 0, the value of the y-axis can be anything, irrespective of the value of the abscissa.
Rules to Find the Reflection in the y-axis
There is no hard rule to find the reflection in the y-axis; you just need to follow these two simple steps, which are given below:
Keep the coordinates of the y-axis fixed
Reverse the sign of the x coordinate
The obtained value of the x coordinate and y coordinate is the reflection of a point on the y-axis.
Solved Examples
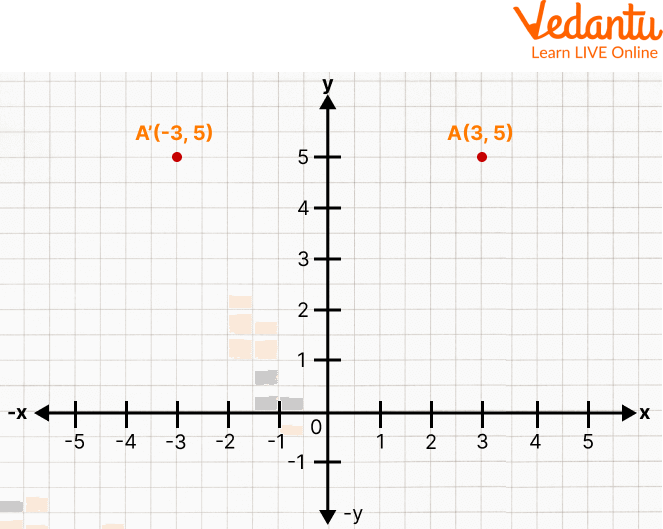
Q 1. Find the reflection of a point on the y-axis of the following:
(3, 5)
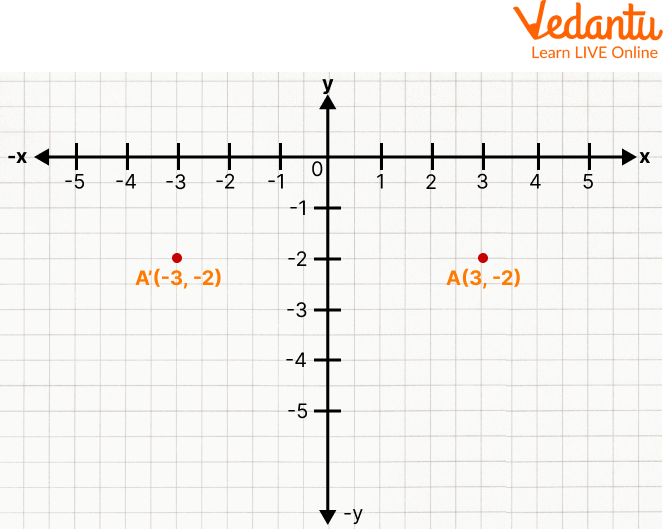
(3, -2)
Ans: For part 1, we need to follow the given steps:
Read the coordinates (3, 5) and find out in which quadrant it lies, i.e. 1st quadrant
Mark the values of x = 3 and y = 5 in the respective quadrants
Highlight the point and write its coordinates
To find its reflection, keep the ordinate same, i.e. 5, and take the additive inverse of the abscissa, i.e. -3
Now, choose the quadrant for the new coordinates, i.e. (-3, 5)
Place the values of x = -3 and y = 5 in the appropriate quadrant
Highlight the point and write its coordinates
This is how you find the reflection of a point (3, 5) on the y-axis.
Reflection of a point in the y-axis
For part 2, we need to follow the given steps:
Read the coordinates (3, -2) and find out in which quadrant it lies, i.e. 4th quadrant
Mark the values of x = 3 and y = -2 in the respective quadrants
Highlight the point and write its coordinates
To find its reflection, keep the ordinate constant, i.e. -2, and take the additive inverse of the abscissa, i.e. -3
Now, choose the quadrant for the new coordinate, i.e. (-3, -2)
Mark the values of x = -3 and y = -2 in the appropriate quadrant
Highlight the point and write its coordinates
This is how you find the reflection of a point (3, -2) on the y-axis.
Reflection on the y-axis
A point on the y-axis of the following is 5 and -2, respectively, the same as the initial given problem.
Practice Problems
Q 1. Locate the reflection on the y-axis of the point (5,6).
Ans. (-5, 6)
Q 2. Find the reflection of a point on the y-axis of the following:
(a) (2, -3)
(b) (-3, 7)
Ans. (a) (-2, -3)
(b) (3, 7)
Q 3. Find the reflection on the y-axis of the points:
(a) (4, 5)
(b) (-1, -2)
Ans. (a) (-4, 5)
(b) (1, -2)
Summary
Summing up here with the concept of reflection in the y-axis. This writing describes all the topics, including rules to find the reflection, graph xy = 1 is reflected in y = 2x, a point on the y-axis has a coordinate, etc. Here we have discussed in depth how to solve the problem based on the reflection of a point in the y-axis. Some practice problems are assigned to the students along with their answers so that they can do more practice and gain proficiency in the concept.
FAQs on Reflection in Y Axis in Coordinate Geometry
1. What is reflection in the y-axis?
Reflection in the y-axis is a transformation that changes the sign of the x-coordinate while keeping the y-coordinate the same. In coordinate geometry, this means any point (x, y) becomes (−x, y) after reflection. It creates a mirror image of the figure across the vertical y-axis without changing its size or shape.
2. What is the rule for reflection in the y-axis?
The rule for reflection in the y-axis is (x, y) → (−x, y). This means:
- The x-coordinate changes sign.
- The y-coordinate remains the same.
This rule applies to all points, shapes, graphs, and functions reflected across the y-axis in coordinate geometry.
3. How do you reflect a point across the y-axis?
To reflect a point across the y-axis, change the sign of its x-coordinate and keep the y-coordinate unchanged. Follow these steps:
- Start with the original point, for example (4, −2).
- Change the x-value to its opposite: −4.
- Keep the y-value the same: −2.
So, the reflected point is (−4, −2).
4. What happens to a graph when it is reflected in the y-axis?
When a graph is reflected in the y-axis, every point (x, y) on the graph becomes (−x, y), creating a mirror image across the y-axis. For functions:
- If the original function is y = f(x),
- The reflected function becomes y = f(−x).
This transformation flips the graph horizontally while preserving its shape and size.
5. What is the formula for reflecting a function in the y-axis?
The formula for reflecting a function in the y-axis is y = f(−x). This means:
- Replace every x in the function with −x.
- The graph will flip horizontally across the y-axis.
For example, if f(x) = x² + 3x, the reflected function is f(−x) = x² − 3x.
6. What is the difference between reflection in the x-axis and reflection in the y-axis?
The difference is that reflection in the x-axis changes the y-coordinate, while reflection in the y-axis changes the x-coordinate.
- X-axis reflection: (x, y) → (x, −y)
- Y-axis reflection: (x, y) → (−x, y)
In simple terms, x-axis reflection flips vertically, and y-axis reflection flips horizontally.
7. Can you give an example of reflection in the y-axis?
Yes, for example, the point (3, 5) reflected in the y-axis becomes (−3, 5). Applying the rule:
- Original point: (3, 5)
- Change x to −3
- Keep y as 5
Final reflected point: (−3, 5).
8. Does reflection in the y-axis change the shape or size of a figure?
No, reflection in the y-axis does not change the shape or size of a figure because it is a rigid transformation. It preserves:
- Lengths
- Angles
- Area
Only the orientation changes, producing a mirror image across the y-axis.
9. How do you reflect a line in the y-axis?
To reflect a line in the y-axis, replace x with −x in its equation. For example:
- Original line: y = 2x + 1
- Replace x with −x: y = 2(−x) + 1
- Simplify: y = −2x + 1
The new equation represents the line reflected across the y-axis.
10. Why does the x-coordinate change sign during reflection in the y-axis?
The x-coordinate changes sign because reflection in the y-axis places each point the same distance on the opposite side of the y-axis. Since distance from the y-axis is measured horizontally:
- Points to the right (positive x) move to the left (negative x).
- Points to the left (negative x) move to the right (positive x).
Thus, (x, y) becomes (−x, y), maintaining equal horizontal distance from the y-axis.
