Definition Types and Methods of Representing Sets with Examples
Set definition: Each set is defined as a group of various items sharing some common trait among themselves. Set members or elements refer to the items that comprise a set. Examples of sets include a collection of cards, a group of automobiles, a group of birds, a group of days of the week, etc. Also, there exist some universally accepted sets like the set of natural numbers, the set of rational numbers, the set of real numbers, the set of integers, the set of whole numbers, the set of irrational numbers, etc.
What is the Cardinality of Sets?
The cardinality of a set is the measure of the size of the set, indicating the number of items contained in that set. It can have both finite and infinite values. The cardinality of the set A = (1, 2, 3, 4, 5, 6) is equal to 6 as set A encompasses six items. Often the cardinality of any set is referred to by the modulus sign appearing on both sides of the set name, for example, |A|.
What are the Methods of Representation of Sets?
Irrespective of the way of representation, every set is named with a capital or an uppercase English alphabet. The set names can be represented, for instance, with the letters A, B, C, D, etc. Small hand or lowercase English alphabets or numeric and other symbols represent the constituent members or the elements of sets. For instance, A = {11, 12, 13, 14, 15}, B={x: x a,c,r,t,f,h,j}
Set representations can be of the following three forms.
Set Builder Form for Representation of Sets
A definite way of describing a set making use of a single element and the statements that illustrate the characteristics of its components, separated by the symbol “:”.
To indicate whether an element is present in the given set or not, we use the Greek letter aphsilon "" . It indicates the phrase “belongs to”.
Again the symbol “∉” is interpreted as "not belonging to."
For example $A=\{x:x\text{ }is\text{ }an\text{ }even\text{ }number,\text{ }x\in N\text{ }and\text{ }x\le 25\}$
Therefore, the set A consists of the elements given by A= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}.
Roster Form for Representation of Sets
Roster form representation refers to the method of expressing a set where the elements of the sets are discretely shown and enclosed within curly braces. The tabular form is another name for this type of set representation.
For example, N= {1,2,3,4,5,6,7,8,9,10,........}
Statement Form for Representation of Sets
Statement form representation refers to the method of denoting a set where the elements of the sets are never discretely shown, but onlt the statement is enclosed within curly braces.
For example, N= {the natural numbers}
What are the Different Types of Sets?
Some of the noteworthy various type so f sets are as follows:
Null set
This defined set contains no elements in it, and hence, is also called an empty set.
Universal Set
A set which contains all the sets defined in a mathematical statemement or problem.
Finite Set
The set whose cardinality is finite.
Infinite Set
The set whose cardinality is infinite.
Superset
By comparing any two sets A and B, if we find every element of the set B is present in set A but every element of set A is not present in the set B, we say that B is a superset of A.
Subset
By comparing any two sets A and B, if we find every element of the set B is present in the set A, we say that B is a subset of A.
Equivalent Set
By comparing any two sets A and B, if we find every element of the set B is present in the set A and vice versa, we say that B is an equivalent set of A and vice versa.
Common Sets of Numbers
The following notations can be used to represent the number sets:
N = Set of Natural numbers
W = Set of Whole numbers
R = Set of real numbers
Q = Set of Rational numbers
Z = Set of Integers
T = Set of Irrational Numbers
What is the Union of Sets?
The union of any two sets namely set P and set Q indicates the elements that are present in either of the sets P and Q. It is indicated symbolically by the statement $P\cup B$.
What is the Intersection of Sets?
The intersection of any two sets, namely set P and set Q indicates the elements that are present in both the sets P and Q. It is indicated symbolically by the statement $P\cap B$
What is a Venn Diagram?
Visual diagrams may be used to depict sets as well. A Venn diagram is the visual representation of a set. In a Venn diagram, the sets are represented graphically or visually as circles, and the intersection of the circles reveals each set's connection. The rectangular region around the sets or circles is referred to as the universal set, while the area inside the circles, or the sets, is referred to as the elements.
Venn diagram representing two sets
There are two sets A and B that overlap one another, as seen in the image above. The items shared by the two sets supplied are shown in this intersection. The universal set, denoted by the letter U, which symbolises all the items that may or may not be present in the sets, is the rectangular area around the sets.
Solved Examples
1. Write the following set statement in both set-builder form and roster form. Set of all natural numbers that lie between 1 and 40 that are prime.
Ans. the above set statement can be represented in following ways:
Set-builder form: A=x| x is prime, 1x40 and xN
Roster form: A=2,3,5,7,11,13,17,19,23,29,31,37
2. Draw the venn diagram for the following:
In a college, 200 students are selected. 120 like tea, 140 like coffee and 50 like both tea and coffee.
Ans. Let T = set of students who like tea
C= set of students who like coffee
n(T) = Cardinality of set T
= 120
n(C) = Cardinality of set C
= 140
n(T\[\cap\]C) = cardinality of students who like both tea and coffee
= 50
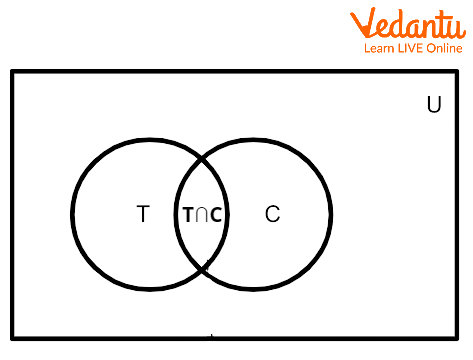
Students who like both tea and coffee
3. Write the set builder Form for A={2,3,4,5,6,7,8,9}
Ans. A={x| x is a natural number and 2x9}
4. Write the following set statement in set-builder form. Set of all whole numbers less than 20 that are composite.
Ans. The above set statement can be represented in following ways:
Set-builder form: $A=\{x:x\text{ }is\text{ }composite,\text{ }0\le x\le 20\text{ }and\text{ }x\in W\}$
5. Write the following set statement in roster form. Set of all whole numbers less than 20 that are composite.
Ans. The above-set statement can be represented in the following ways:
Roster form: $A=A=4, 6,8,9,10,12,14,15,16,18,20$
Summary
The sets represent the statements that can define the relationship among the elements given in a group.
The sets can be displayed in three ways: set-builder, statement form and roster form.
The cardinality of sets indicates the number of elements in a set, which can be infinite or finite.
The visual representation of sets makes use of Venn diagrams to show the correct relationship among the sets.
Practice Problems
Q1. Write the following set statement in both set-builder form and roster form. Set of all even prime numbers.
Q2. Write the following set statement in both set-builder form and roster form. Set of all odd prime numbers less than 100.
Q3. Write the following set statement in both set-builder form and roster form. Set of all even composite numbers between 200 and 300.
List of Related Articles
FAQs on Sets and Their Representations in Mathematics
1. What is a set in mathematics?
A set in mathematics is a well-defined collection of distinct objects called elements. The objects inside a set are known as elements or members.
- Sets are usually written using curly brackets: { }.
- Example: A = {1, 2, 3, 4}.
- Each number inside the brackets is an element of the set.
2. What are the different ways to represent a set?
A set can be represented using roster form, set-builder form, or a Venn diagram.
- Roster form: List all elements explicitly. Example: A = {2, 4, 6}.
- Set-builder form: Describe elements using a rule. Example: A = {x | x is an even number less than 8}.
- Venn diagram: A pictorial representation using circles to show relationships between sets.
3. What is roster form in sets with an example?
The roster form of a set lists all its elements inside curly brackets separated by commas.
- Example: If B is the set of vowels in English, then B = {a, e, i, o, u}.
- Elements are written only once, even if repeated.
4. What is set-builder form in sets?
The set-builder form defines a set by stating a property that its elements satisfy.
- General form: A = {x | condition on x}.
- Example: A = {x | x is a natural number less than 5}.
- This represents A = {1, 2, 3, 4}.
5. What is a Venn diagram in set theory?
A Venn diagram is a graphical representation of sets using circles to show relationships between them.
- Each circle represents a set.
- Overlapping regions show common elements (intersection).
- The rectangle around circles represents the universal set.
6. What is the difference between roster form and set-builder form?
The main difference is that roster form lists elements explicitly, while set-builder form describes elements using a rule or condition.
- Roster form example: A = {1, 2, 3}.
- Set-builder form example: A = {x | x is a natural number less than 4}.
7. What is a finite and infinite set?
A finite set has a limited number of elements, while an infinite set has unlimited elements.
- Finite example: A = {1, 2, 3} (3 elements).
- Infinite example: N = {1, 2, 3, ...} (natural numbers).
8. What is the cardinality of a set?
The cardinality of a set is the number of elements it contains.
- It is denoted by n(A) or |A|.
- If A = {2, 4, 6, 8}, then n(A) = 4.
9. What is an empty set and how is it represented?
An empty set is a set that contains no elements.
- It is represented by ∅ or { }.
- Example: The set of natural numbers less than 0 is ∅.
10. What is a universal set in set theory?
The universal set is the set that contains all elements under consideration in a particular context.
- It is usually denoted by U.
- All other sets discussed are subsets of U.
- In Venn diagrams, it is represented by a rectangle enclosing all sets.
