Tan 90 Degrees and Its Exact Trigonometric Meaning

One of the fundamental trigonometric functions and one that is quite frequently employed in trigonometry is the tangent. The ratio of the sine and cosine functions can be used to define the tangent function. The ratio of the perpendicular to the base of the triangle serves as the formula for the tangent function in a right-angled triangle. It can alternatively be written as the cotangent function reciprocal. In this article, we are going to study the Tan $90$ degrees formula, how to find it and what is a $90$ degrees angle.

Tan Definition

The most significant trigonometric function after Sin and Cos is Tan. The opposing side's length divided by the adjacent side's length is the angle's tan function. It is simple to determine the values of these tangent functions using a right-angled triangle. In a right-angled triangle, the side that forms a side of both the angle of intersection and the right angle is known as the adjacent side. In contrast, the side that forms the opposite of the angle of intersection is known as the opposite side and the hypotenuse side is known as the hypotenuse side. Tan gives the slopes of straight lines, for example: the straight line drawn in the x-y coordinate plane. The Tangent can also be represented as tan.

Tangent Function

Tan Formula

• For a given right-angled triangle, Tan is defined as the ratio of the opposite side and the adjacent side,

such as $\tan \theta = \dfrac{{BC}}{{AB}}$ and the other formula for tangent function can be written as $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ .

To prove this we have,

$\tan \theta = \dfrac{{BC}}{{AB}}$

We can also write,

$\tan \theta = \dfrac{{\dfrac{{BC}}{{AC}}}}{{\dfrac{{AB}}{{AC}}}}$

As, $\sin \theta = \dfrac{{BC}}{{AC}}$ and $\cos \theta = \dfrac{{AB}}{{AC}}$ .

So, using these in the tangent formula, we get

$ \Rightarrow \tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$

Thus, we can get the values of tan ratio for the specific angles

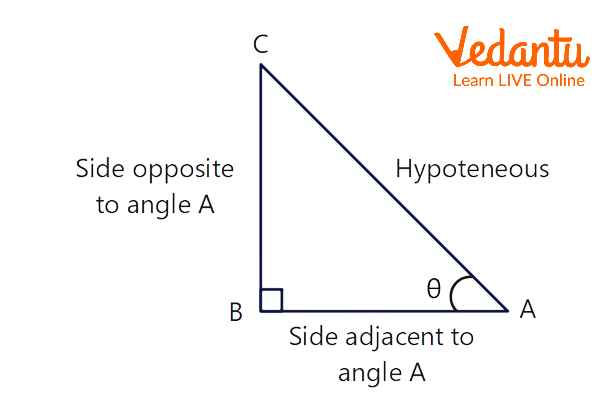
Right-angled Triangle

• In Triangle we can find the tan value by dividing the opposite and adjacent sides of the triangle where \[\theta \] is the angle of the triangle.

• Therefore, tan formulas are $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ and $\tan \theta = \dfrac{{BC}}{{AB}}$ .

90-Degrees Angle

An angle of $90$ degrees is created when two straight lines cross perpendicularly. In other words, the angle between two radii of a circle that results in the circumference of the circle being cut off by an arc with a length equal to one-quarter of the circumference; also known as a $90^\circ $ angle or $\dfrac{\pi }{2}$ radian.

Example: The hands of a clock at 3 o’clock and at 12 o’clock.

The four angles of simple geometries like squares and rectangles are always at $90$ degrees. When two lines intersect at a $90$ degree angle, the lines are referred to as perpendicular lines.

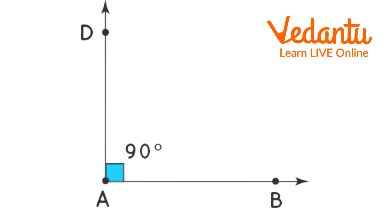
90-Degree Angle

What is Tan 90

For tan $90$ degrees, the angle $90$ degree always lies on the positive y-axis and the tangent function is a periodic and odd function, we can represent tan 90 degrees as $\tan \left( {90^\circ + n \times 180^\circ } \right)$, $n \in \mathbb{Z}$. If the question arises, why is tan 90 undefined? Since the outcome is infinite and we cannot define infinity, tan 90 is an indefinite quantity.

Methods to Find Tan 90 Degrees Exact Value

There are two methods to find the tan value, namely

• Using Unit circle

• Using Trigonometric functions

Using Unit Circle

To find the value of tan $90$ degrees using unit circle:

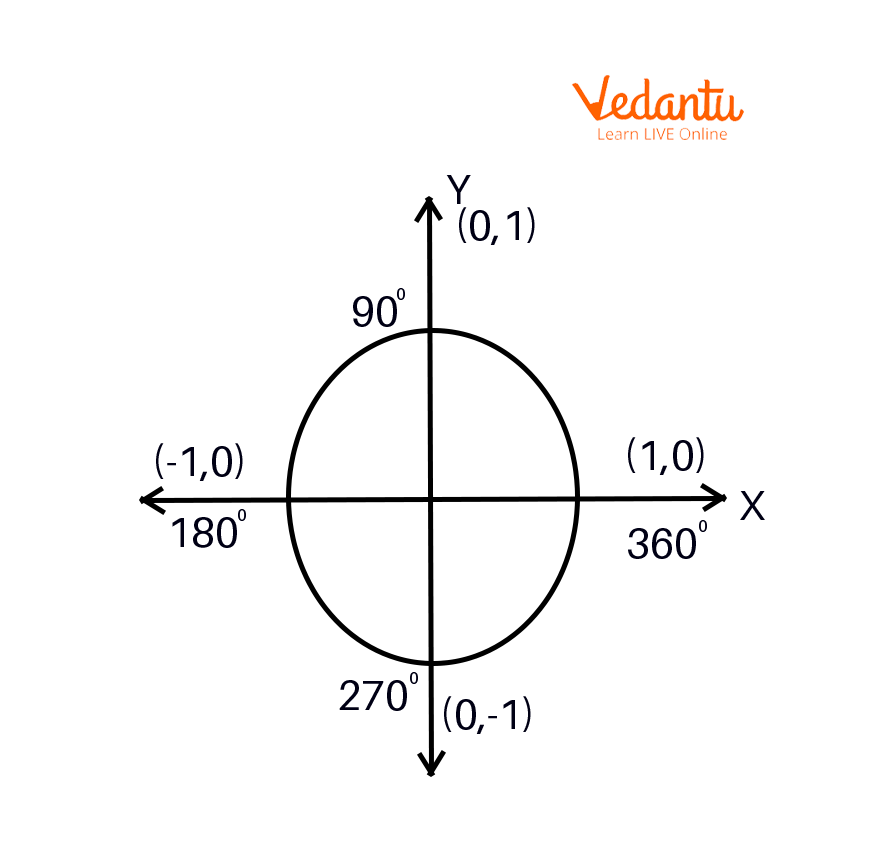
Unit circle

First we need to rotate ‘$r$’ anticlockwise to form a $90$ degree angle with the positive x-axis. The tan of $90$ degrees equals the y- coordinate $(1)$ divided by x- coordinate $(0)$ of the point of intersection $(0,1)$ of the unit circle and $r$. And tan is represented in the third quadrant of the circle with $360$ degree.

Therefore the value of $\tan 90^\circ = \dfrac{y}{x} = \dfrac{1}{0} = \infty $ .

Using Trigonometric Functions

The tangent function is one of the six primary functions in Trigonometry. The tangent formula is given as tan A $ = $ opposite side divided by the adjacent side.

• Tan $90$ degree can also be found by using the sine and cosine terms

Example: $\tan 90^\circ = \dfrac{{\sin 90^\circ }}{{\cos 90^\circ }}$.

Whereas \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \] which can be written as

\[\sin \theta =\sqrt{1-{{\cos }^{2}}\theta }\] and similarly

\[\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }\] then we can define tan 90 degree by

$\tan 90^\circ = \dfrac{{\sqrt {1 - {{\cos }^2}90^\circ } }}{{\cos 90^\circ }}$ or $\tan 90^\circ = \dfrac{{\sin 90^\circ }}{{\sqrt {1 - {{\sin }^2}90^\circ } }}$ .

• Then by using cot function, we can define tan $90$ degree as tan 90 is equal to

$\dfrac{1}{{\cot 90^\circ }}$.

• We can use Trigonometric identities to represent tan 90 degrees as $\tan (180^\circ - 90^\circ ) = - \tan 90^\circ $. This means that in the second quadrant, the value of the tangent function will be negative.

$\cot (90^\circ - 90^\circ ) = \tan 90^\circ $. This says that the cotangent function in the very first quadrant will change to the positive tangent value.

$[\cot (90^\circ + 90^\circ ) = - \tan 90^\circ ]$ . This implies that in the second quadrant, the value of the cotangent function will change to negative times the value of the tangent function.

Similarly, we can define tan $90$ degree in many terms with six trigonometric functions for each quadrant system.

Since the $90$ degree always lies on the positive axis of y so the value will be undefined.

Interesting Facts

• The word tangent comes from the name tangerine, is “to touch”.

• Babylonians invented the measurement of the angle.

• The Mesopotamians passed their base-60 numerical system to the ancient Egyptians, who used it to divide the circle into $360$ degrees.

Solved Examples

1. What is the value of tan 90 degrees using the functions sin \[{{90}^{0}}\] and cos \[{{90}^{0}}\]?

Solution:

We know that

$\tan 90^\circ = \dfrac{{\sin 90^\circ }}{{\cos 90^\circ }}$

Substituting the values of sine $90$ degree and cosine $90$ degree in the above equation, we get

$\tan 90^\circ = \dfrac{1}{0} = \infty $ .

2. Find the value of tan $45$ degree using the function sin \[{{45}^{0}}\] and cos\[{{45}^{0}}\]?

Solution:

We know that

$\tan 45^\circ = \dfrac{{\sin 45^\circ }}{{\cos 45^\circ }}$

$ \Rightarrow \tan 45^\circ = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}}$

$ \Rightarrow \tan 45^\circ = 1$.

3. What is the value of tan 90 degrees by using cot \[{{90}^{0}}\]?

Solution:

We know that

Tan 90 degree $ = \dfrac{1}{{\cot 90^\circ }}$ .

Where, $\cot 90^\circ = 0$

Then tan 90 degree $ = \dfrac{1}{0} = \infty $ (or undefined).

4. Find tan A with the opposite side $ = 25$ and adjacent side $ = 5$?

Solution:

We know that

Tan A $ = $ opposite side divided by the adjacent side

Tan A $ = \dfrac{{25}}{5}$

Tan A $ = 5$.

Summary

The tangent of the angle is the trigonometric ratio between the adjacent and opposite sides of a right triangle containing that angle. The value of Tan 90 degrees always lies on the positive y-axis, so it is undefined. We also talked about ways to find tan values for any given angle and sides.

Practice Questions

1. Find the Value of Tan B where the opposite side and adjacent side of the functions are 3 and 6.

2. Find the value of Tan 45 degrees by using the function cot 45 degrees.

3. Find the value of Tan 60 degrees by using the function sin \[{{60}^{0}}\] and cos\[{{60}^{0}}\]?

Answers:

1. $\dfrac{1}{2}$

2. $1$

3. $\sqrt 3 $