




Overview of Transformations
In normal words transformation means a mathematical function. You can say that a transformation is the invertible function from any set X to its own set X or any other set Y. For any term the transformation may simply indicate that the geometric aspect of this particular function is considered. Further these transformations are of many types. In layman's terms you can say that's means just taking a preimage and then transforming it or producing it into an actual image.
Thus when an object is transformed from its one form to another form then both the object and image can be congruent or they can be just similar.
When the shape of an object can easily be transformed to another shape just by using turns, flips or slides then both the shapes can be known as congruent while when one shape needs to be resized to form the another shape then we can refer to it as similar shapes.
This article provided to you by Vedantu will help to clear your doubts and queries related to the topic transformations. At Vedantu our main goal is to make the students proud of any topic they learn, so in order to be well aware of the topic, the students are provided with frequently asked questions at the end of this article in order to clear most of their queries regarding the topic Transformation.
In this article you are going to learn about this topic transformation in mathematics which is the base of your mathematics if higher classes. In this article the topics that you will come across are transformation, definition of transformation , categories of Transformation,types of transformation and finally the conclusion. Let's have a look at this article in order to get a better knowledge of the transformation topic.
In geometrical terms, when objects move in the coordinate plane, they go through transformations. In other terms, a set of coordinate points change into a different set of coordinates by the process of transformation. As in English, “transformation” means “to change,” in geometry, it refers to changes in the geometric properties of an object. There are different kinds of transformations that can occur; some of them do not change the size of the object while some of the transformations resize the original object. We will look at the different kinds of transformation in this article with examples.
What is Transformation in Maths?
According to Merriam - Webster dictionary, transformation means “an act, process, or instance of transforming or being transformed”. In maths, transformations are rotations, reflections, and translations of forms on a coordinate plane. Felix Klein proposed a new perspective on geometry known as transformational geometry in the nineteenth century. The majority of geometric proofs are dependent on object transformations. Transformations allow us to change any image in a coordinate plane.
The transformation is a function, f, that maps to itself, i.e. f: X → X. After the transformation, the pre-image X becomes the picture X. Any or a combination of operations such as translation, rotation, reflection, and dilation can be used in this transformation. Transformation is the act of moving a function in one direction, rotation is the act of spinning a function around a point, reflection is the function's mirror image, and dilation is the act of scaling a function. In mathematics, transformations describe the movement of two-dimensional figures around a coordinate plane.

Transformations in Maths
Categories of Transformation
A transformation can be broadly categorised into 2 different types:
Rigid or isometric Transformation – The transformation in which size of the pre-image is unchanged is called a rigid transformation. If you look at this transformation then you are not going to find any change in the form,that is the shape and size of the object.
Non-Rigid or non-isometric Transformation – A transformation that will change the size, but not the shape of the pre-image is called a non-rigid transformation. If you look at this transformation then you are not going to find any change in the form,that is the shape and size of the object.
Different Types of Transformations in Mathematics
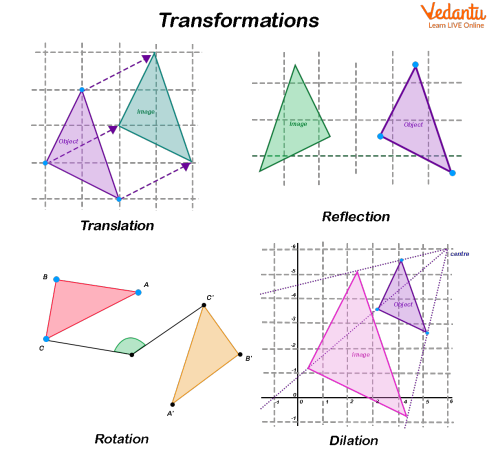
Types of transformations
There are four types of transformations - translation, rotation, reflection, and dilation. Out of these, rotation, translation and reflection are rigid transformations. Rigid transformations keep the length and angle measurements, as well as the perimeter and area intact. The picture and the preimage are congruent. Dilation is non rigid transformation. Angle measure is the only thing that non-rigid transformations keep. The perimeter and side lengths are not equal, but they are in proportion. The picture and the preimage are remarkably similar.
Translation — A translation moves the figure away from its original coordinate plane position without changing its orientation.
Rotation — The image is the preimage rotated around a fixed point; "a turn."
Reflection — Consider cutting out a preimage, lifting it, and repositioning it face down. That's called a reflection or a flip. A reflection image is a reflection of the preimage.
Dilation — The image is a larger or smaller version of the preimage; "shrinking" or "enlarging." To dilate a polygon's preimage, duplicate its interior angles while increasing each side proportionally.
Rules of Transformation
Transformation is represented algebraically and graphically. Algebraic functions often include transformations. Rather than tabulating the coordinate values, we can use the formula of transformations in graphical functions to obtain the graph simply by transforming the basic or parent function and thus moving the graph around. Transformations assist us in visualising and learning algebraic equations.
Conclusion
When a geometric figure is moved around on a coordinate plane, then transformations happen. Transformations do not change the shape of an object but can change its position, size, or orientation. Transformation can be rigid or isometric, where the size of the image does not change, or they can be non-rigid or non-isometric when the size of the image changes due to the transformation. Transformations are mostly done on a coordinate plane, as it makes it easy to count and draw. A common and easiest way of performing transformation is by performing the required operation on the vertices of the preimage, and when you connect the dots, you will be able to get the final transformed image.
FAQs on Transformations – Overview, Definition, Categories and Types
1. When do we say 2 Shapes are Congruent?
Any object whose shape we want to transfer and even we are able to change the shape of that object. This means any time one shape can be transformed into another shape maybe with numerous methods . They can be either flips, most commonly called reflections, turns, commonly known as rotations, or slides that we call as translations. If by any of these methods shapes can be transformed from one to another then both the shapes you can refer to as congruent shapes.
2. When do we say 2 Shapes are Similar?
Two shapes are said to be similar, the case in which the shapes can be called similar are when we are required to resize a shape or dilate that shape just in order to get any other shape. You can achieve this resizing and dilating or other change in shape either by turning, flipping or sliding the shapes so that the new shape can be formed which is similar to the previous one.bin transformation topic you learn about how to transform them in detail.
3. What are the Different Categories of Transformations?
Transformations are classified into 2 types: rigid or isometric and non-rigid or non-isometric. In the rigid transformation size of the object does not change but in non-rigid transformation, the size of the object is either enlarged or reduced. If you are looking for a type of transformation in which there should not be any change in the shape and size then consider the rigid transformation otherwise non rigid transformation includes the change in the shape and size of the object.
4. What are the Different Types of Rigid Transformations?
The rigid transformations are rotation, translation, reflection, and glide reflection. If we talk about translation then objects can be transferred only by sliding it. In rotation the object is turned around a fixed point that we call as the centre point. In reflection a mirror image if the object along the line is formed. In glide reflection the final image we receive also goes through transformation. In these kinds of transformation you will nor see any change IN the shape the object is transformed into without change in shape or size.
5. What are the Different Types of Non-Rigid Transformations?
There is only one non-isometric or non-rigid transformation called dilation. It is also called expansion, contractions, compressions, or enlargement. Talking about non rigid.transformation there is change in the shape and size if hge object. I'd we look at enlargement the object's size will increase. In expansion the rise increases and body expands on contraction the size decreases and object contracts while in compression the object is compressed to cause decrease in size. These transformations lead to change in shape.
6. How do you Perform a Transformation?
The most known way to perform a transformation on a shape is by doing the requested operation on the vertices of the preimage and then joining the dots to get the image. For any specified transformation you are provided with certain instructions you need to have a look at that information and then perform the transformation. It may cause change in shape or size or may not cause any change in shape or size of the object to be transformed.
7. What is a “Mirror Line” in the Context of Transformations?
In the reflection transformation the shape is flipped along a line which is called the “mirror line” and all the points on both the preimage and the image are at equal distance from the mirror line. This mirror line you will hear most probably in the reflection kind of transformation. Remember that reflection is a kind of transformation where the shape and size of the object is not changed, just the image is a reflection of the object.
8. What is a Glide Reflection and How is it Different from Reflection Transformation?
A glide reflection is the one in which the shape is flipped across the mirror line and then some kind of slide or translation is done on the shape. So glide reflection is different from reflection as it involves “reflection + translation.” In glide reflection also there is no change in shape or size of the object. It is a further reflection of the already formed image by the reflection of the object. In reflection only once the object is transformed to image but in this two times the reflection us phone to form the final image
9. What are rigid and non-rigid transformations?
When creating an image, a rigid transformation does not change the size or shape of the preimage. Three transformations are rigid. Reflection, rotation, and translation are examples of rigid transformations. The image will not change in size or shape as a result of these transformations.
A non-rigid transformation can change the size or shape of the preimage or both. Non-rigid transformations include dilation and shear. The image will change in size, shape, or both as a result of the transformation.
10. What do you mean by Shear?
Shearing a figure entails fixing one line of a polygon and moving all the other points and lines in a specific direction, proportional to their distance from the fixed line. Shear can be seen in italic letters on a computer.











