




Parabola: Introduction
A tangent to a parabola is only possible when the condition of tangency is satisfied. Different types of parabolas have different conditions of tangency. To represent a tangent to a parabola, there are three forms: Point, Slope and Parametric Forms. One needs to solve the equation of tangent and parabola, try to eliminate the variable, and use the discriminant rule ${b}^{2} = 4ac$ if the equation of a parabola is in a general form.
In this article, we will understand the concept of a tangent to a parabola and the different forms of the parabola. Solve some questions regarding the different forms of a tangent to a parabola.
Different Types of Parabolas and Their Graphical Representation
There are several parabolas. The first type of parabola is when the origin of the parabola is at the origin $(0,0)$, and the other type is the general parabola, where the centre of the parabola is anywhere.
Upward parabola (Faces upward)
Downward parabola (Faces downward)
Right parabola (Faces right)
Left parabola (Faces left)
General parabola
Starting with the common standard upward parabola, The equation of an upward parabola is ${x^2} = 4ay$, where $a$ is the distance of focus from the origin. The graph of the upward parabola is as follows,
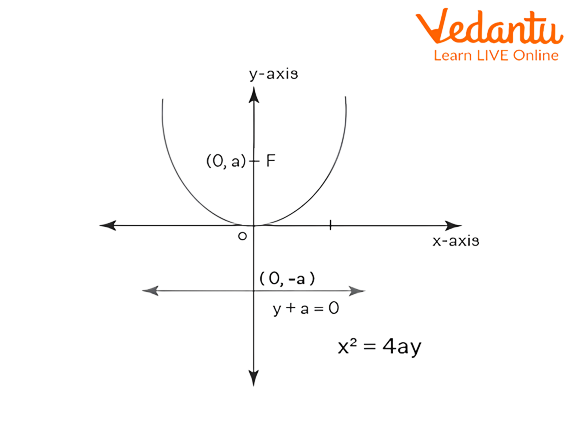
Graphical representation of upward parabola.
The equation of the right parabola is ${y^2} = 4ax$. The graph of the right parabola is as follows,
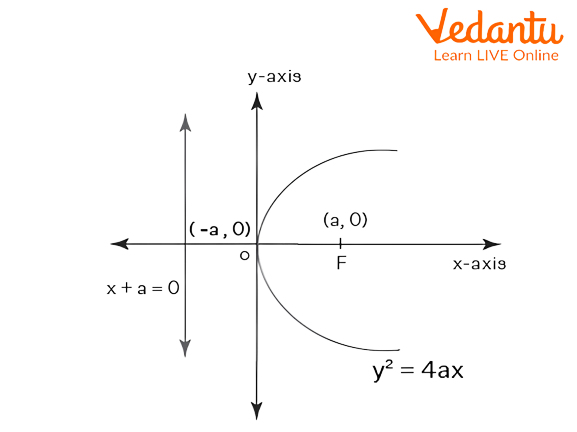
Graphical representation of right parabola.
The equation of the left parabola is ${y^2} = - 4ax$. The graph of the left parabola is as follows,
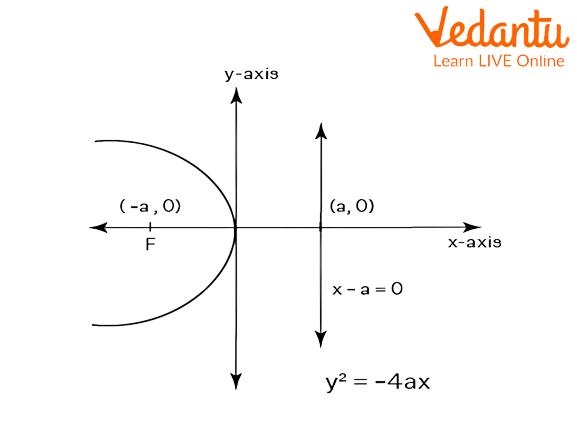
Graphical representation of left parabola.
The equation of the downward parabola is ${x^2} = - 4ay$. The graph of the left parabola is as follows,
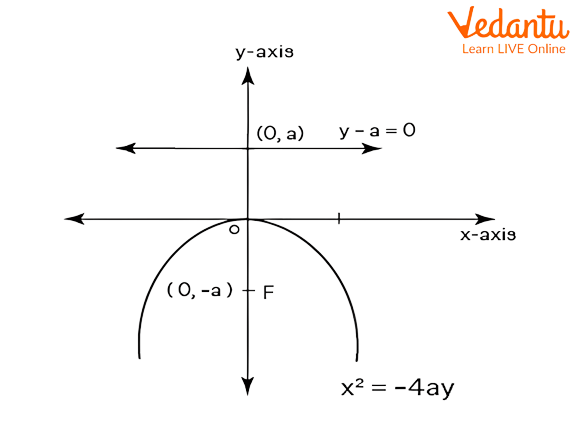
Graphical representation of downward parabola.
The equation parabola at center $(h,k)$ will be $y = a{{(x - h)}^2} + k$.
Condition of Tangency of a Parabola
It is necessary to adhere to the tangency condition to draw a tangent to a parabola. Finding the tangent to a parabola requires adhering to three different sorts of conditions, especially for right, upward, and parametric forms.
The condition of tangency are as follows:
The line \[y = mx + c\] is a tangent to a parabola ${y^2} = 4ax$ only if $c = \dfrac{a}{m}$.
The line $y = mx + c$ is a tangent to a parabola ${x}^{2} = 4ay$ only if $c = - a{m^2}$.
The line $x\cos \theta + y\sin \theta = p$ is a tangent to a parabola ${y^2} = 4ax$ only if $\sin 2\theta + p\cos \theta = 0$.
Various Forms of Tangent to a Parabola
There are various forms of the tangent to a parabola. If the equation of a parabola is given in the standard form. Then, the equation of a tangent to parabola can be easily found by following the given steps:
First, you need to find the point of intersection of the parabola and tangent and the slope of the tangent.
The slope of the tangent is given by differentiating the equation of a parabola and putting the point of intersection on the derivative.
Then, use the Point-slope form of a line to write the equation of tangent.
There are three forms of a tangent to a parabola, Slope form, Point form, and Parametric form.
Slope form of Tangent to a Parabola: In slope forms, the equation of tangent must be written in the slope-intercept form of a line. The line $y = mx + \dfrac{a}{m}$ is a tangent to a parabola ${y^2} = 4ax$. Similarly, if the parabola is ${x^2} = 4ay$, then the equation of tangent will be $y = mx - a{m^2}$.
Point Form of Tangent to Parabola: In point form, the equation of a tangent to a parabola ${y^2} = 4ax$ at some point $({x_1},{\rm{ }}{y_1})$ is given by $y{y_1}\; = {\rm{ }}2a(x{\rm{ }} + {\rm{ }}{x_1})$.
The parametric form of Tangent to a Parabola: In parametric form, the equation of a tangent to parabola ${y^2} = 4ax$ at $(a{t^2},2at)$ is given by $ty = x + a{t^2}$.
Example: Write the equation tangent to a parabola with equation ${y^2} = 16x$ at $(1,4)$ in slope form.
Solution: Comparing the equation of the parabola with the standard equation and differentiating the equation to get the slope of the line:
By comparing the equation with the standard equation, we get
$\begin{array}{l}{y^2} = 4 \times 4x\\a = 4\end{array}$Differentiating the curve equation,
$\begin{array}{l}\dfrac{{d({y^2})}}{{dx}} = \dfrac{{d(16x)}}{{dx}}\\2y\dfrac{{dy}}{{dx}} = 16\\\dfrac{{dy}}{{dx}} = \dfrac{8}{y}\\{\dfrac{{dy}}{{dx}}_{(1,4)}} = \dfrac{8}{4}\\m = 2\end{array}$Now, using the condition of tangency of the parabola,
$\begin{array}{l}c = \dfrac{a}{m}\\c = \dfrac{4}{2}\\c = 2\end{array}$So, the equation of a tangent to parabola in slope form is $y = 2x + 2$.
Point of Contact of Tangent and Parabola
The point of contact between the tangent and parabola is a point where the tangent and curve meet. The point of contact is easily given by following some basic steps:
First, you have to solve the tangent equation and a parabola equation.
The value of $x$ and $y$ is the point of contact.
The point of contact of tangent $y = mx + \dfrac{a}{m}$ right parabola ${y^2} = 4ax$ is $\left( {\dfrac{a}{{{m^2}}},\dfrac{{2a}}{m}} \right)$.
The point of contact of tangent $y = mx - a{m^2}$ right parabola ${x^2} = 4ay$ is $\left( {2am,a{m^2}} \right)$.
Where a is the length of focus and $m$ is the slope of the tangent.
Example: Verify the condition of tangency and find the point of contact of tangent $3x + 4y = 5$ to a parabola $80y = - 9{x^2}$.
Solution: First, verify the condition of tangency and then find the point of contact:
Finding the value of $a$,
$\begin{array}{l}9{x^2} = - 80y\\{x^2} = - \dfrac{{80}}{9}y\\{x^2} = - 4 \times \dfrac{{20}}{9}y\end{array}$
Hence, the value of $a$ is $\dfrac{{20}}{9}$.Now, finding the intercept and slope of a given tangent by writing it in slope-intercept form,
$\begin{array}{l}3x + 4y = 5\\4y = - 3x + 5\\y = - \dfrac{3}{4}x + \dfrac{5}{4}\end{array}$
Hence, the slope of the tangent is $ - \dfrac{3}{4}$ and the intercept is $\dfrac{5}{4}$.The condition of tangency is $c = a{m^2}$, putting the values.
$\begin{array}{l}\dfrac{5}{4} = \dfrac{{20}}{9} \times {\left( { - \dfrac{3}{4}} \right)^2}\\\dfrac{5}{4} = \dfrac{{20}}{9} \times \dfrac{9}{{16}}\\\dfrac{5}{4} = \dfrac{5}{4}\end{array}$
Hence, the condition of tangency is verified.
Now, the point of contact of a tangent to the parabola is given as $\left( {2am,a{m^2}} \right)$. Putting the values,
$\left( {2 \times - \dfrac{{20}}{9} \times - \dfrac{3}{4}, - \dfrac{{20}}{9}{{\left( { - \dfrac{3}{4}} \right)}^2}} \right) = \left( {\dfrac{{10}}{3}, - \dfrac{5}{4}} \right)$
Hence, the point of contact of parabola and tangent is $\left( {\dfrac{{10}}{3}, - \dfrac{5}{4}} \right)$.
Solved Problems
Q.1 Find the equation of tangent to parabola $x = 14t;y = 7{t^2}$ at $t = 3$.
Ans. Given: The Parametric equation of parabola is $x = 14t;y = 7{t^2}$ .
To find: The equation of tangent.
By looking at the equation of the parabola, it is clear that the parabola is upward.
We know that the condition of tangency of an upward parabola is $c = - a{m^2}$.
By comparing the equation of parabola with standard equation $x = 2at;y = a{t^2}$, we get
$a = 7$
The point of contact of tangent and parabola is $(a{t^2},2at)$.
$\begin{array}{l}(a{t^2},2at)\; = \left( {7 \cdot {3^2},2 \cdot 7 \cdot 3} \right)\\ = (63,42)\end{array}$
Now, using the parametric form of tangent to a parabola $ty = x + a{t^2}$,
$\begin{array}{l}ty = x + a{t^2}\\3y = x + 7{(3)^2}\\3y = x + 63\\y = \dfrac{1}{3}x + 21\end{array}$
Hence, the equation of tangent is $y = \dfrac{1}{3}x + 21$.
Q.2 Find the point of contact of tangent $y = 5x + \dfrac{4}{5}$ to a parabola ${y^2} = 20x$.
Ans. Given: The equation of parabola is ${y^2} = 20x$ and the equation of tangent is $y = 5x + \dfrac{4}{5}$.
To find: The point of contact of tangent and parabola.
The point of contact of a tangent to a parabola is given by $\left( {\dfrac{a}{{{m^2}}},\dfrac{{2a}}{m}} \right)$.
By comparing the equations with standard forms, we get
$\begin{array}{l}a = 4\\m = 5\end{array}$
Putting the values in standard point of contact,
$\begin{array}{l}\left( {\dfrac{a}{{{m^2}}},\dfrac{{2a}}{m}} \right) = \left( {\dfrac{4}{{{5^2}}},\dfrac{{2(4)}}{5}} \right)\\ = \left( {\dfrac{4}{{25}},\dfrac{8}{5}} \right)\end{array}$
Hence, the point of contact of tangent and parabola is $\left( {\dfrac{4}{{25}},\dfrac{8}{5}} \right)$.
Summary
The tangent to a parabola can be written in point form, slope form and parametric form. In point slope-form, the line $y = mx + \dfrac{a}{m}$ is a tangent to a parabola ${y^2} = 4ax$. Similarly, if the parabola is ${x^2} = 4ay$ then the equation of tangent will be $y = mx - a{m^2}$.
In point form, the tangent equation to a parabola ${y^2} = 4ax$ at some point $({x_1},{\rm{ }}{y_1})$ is given by $y{y_1}\; = {\rm{ }}2a(x{\rm{ }} + {\rm{ }}{x_1})$ and in parametric form, the equation of a tangent to parabola ${y^2} = 4ax$ at $(a{t^2},2at)$ is given by $ty = x + a{t^2}$.
Each form of the equation of tangent has some advantages. If the equation is given in a parametric form and also some value is given as a parameter, then using the parametric form of a tangent, the equation of tangent can be written easily. If a point is given, then the point form of the tangent to the parabola easily gives the equation.
Practice Questions
Verify the condition of tangency for parabola $y = 36{x^2}$ and the tangent $y + 9 = x$.
Ans. The condition can be verified by finding the value of slope and focal distance.
Find the equation of a tangent to a parabola $y = 56{x^2}$ with a slope equal to $7$, in slope form.
Ans. y=7x-686
List of Related Articles
FAQs on Various Forms of Tangents in Parabola
1. Can a tangent intersect the parabola at more than one point?
No, a tangent to any curve can intersect the curve at only one point.
2. Can tangent lines cross through the graphs or not?
A tangent line only appears at one location on a graph, and that location's slope is the same as the graph's overall slope. Visually, the graph at x = a bounces off the tangent line to f at a: Some points on the graph may also have tangent lines that pass through them.
3. What is the tangent to a parabola at its vertex in slope form?
As there will be either a maximum or a minimum at the parabola's vertex, the tangent at that point will be a straight line. The equation will be $y = {y_o}$ in slope form.























