Vector Equations

In this article, we will get to know the vector equations as well as solve examples for better understanding. We use vector equations to represent the lines or planes with the help of variables in three dimensions. We will learn about the different expressions for the equation of a plane in vector form. When we need to find the location of an object to another, we do this with the help of Position Vector. Also, a zero vector is a unique vector.

Vector Equation

A vector is nothing but an object or a geometric entity that has direction and length (magnitude). A vector equation involves a linear combination of vectors with possibly unknown coefficients. It is used to represent lines or planes in 3D. As we know, a vector in a plane is represented by an arrow (a line segment).

The initial and terminal point is called the endpoints of the segment. The direction of the vector is known from the initial to the terminal point of an arrow. We learn about the magnitude from the length of the line segment. Also, the different vector equations are in the:

i) A Line

ii) A Plane

Equation of a Plane and its Different Forms

As we know, a line is 1D which has no width but only length. And a plane is a 2D ruled surface spanned by two linearly independent vectors. Also, one normal and one point are sufficient to form the plane equation. It represents a plane surface in a 3D space.  We use different methods based on the given inputs. Next, we know that there are two forms of the equation of a plane. They are

i) The Vector form 

ii) The Cartesian form

Different Expressions of Vector Equations of a Line

As we know, the vector equations of a line can be obtained with the help of any two points on the line or with the help of a point on the line and a parallel vector. There are two methods of forming a vector equation of a line:

i) The vector equation of a line pass through a point and have a position vector \[\overrightarrow{a}\]and parallel to vector line \[\overrightarrow{b}\]is \[\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}\].

ii) The vector equation of a line pass through two points with the position vectors\[\overrightarrow{a}\]and \[\overrightarrow{b}\]is \[\overrightarrow{r}=\overrightarrow{a}+\lambda \left( \overrightarrow{b}-\overrightarrow{a} \right)\].

Different Expressions of Vector Equations of a Plane

There are four different expressions/methods for the equation of a plane in vector form used based on the input's value about the plane:

i) Normal Form: We have an equation of a plane at a perpendicular distance (d) from the centre (origin) and having normal unit vector (\[\widehat{n}\]) is\[\overrightarrow{r}\cdot \widehat{n}=d\].

ii) Perpendicular to a Line through a Point: The equation of a plane perpendicular to a given vector \[\overrightarrow{N}\] passing through a point \[\overrightarrow{a}\] is \[(\overrightarrow{r}-\overrightarrow{a})\cdot \overrightarrow{N}=0\].

iii) Three Non-Collinear Lines: When the equation of the plane passing through three non-collinear points\[\overrightarrow{a}\], \[\overrightarrow{b}\] and \[\overrightarrow{c}\] are \[(\overrightarrow{r}-\overrightarrow{a})\left[ (\overrightarrow{b}-\overrightarrow{a})\times (\overrightarrow{c}-\overrightarrow{a}) \right]=0\].

iv) Two planes intersection: Equation of a plane passing through the intersection of two planes, i.e. \[\overrightarrow{r}\cdot \widehat{{{n}_{1}}}={{d}_{1}}\] and \[\overrightarrow{r}\cdot \widehat{{{n}_{2}}}={{d}_{2}}\] is \[\overrightarrow{r}\cdot (\overrightarrow{{{n}_{1}}}+\lambda \overrightarrow{{{n}_{2}}})={{d}_{1}}+\lambda {{d}_{2}}\].

Importance of Zero (Null) Vectors and Non-Zero Vectors

A vector that has zero magnitudes and no direction or undefined direction in an n-dimensional space is called a Zero/Null vector. This means all the components are equal to zero.

Vector and Zero Vectors

Next, we know that distance is a scalar quantity and displacement is a vector quantity. And the importance of zero vectors is that the arbitrary direction (west) in which the man is facing is known even if the displacement is a null vector. So, it is symbolized as:

i) In 3D by \[\overrightarrow{0}=(0,0,0)\]

ii) In 2D by \[\overrightarrow{0}=(0,0)\]

Thus, a null vector is an additive identity in vector algebra.

Next, a vector with a non-zero magnitude is called a non-zero vector. This means that a component is equal to zero but all its components cannot be zero all the same time.

The Angle between Two Vectors

When there is an intersection of tails and an angle is formed and this is called the angle between two vectors. Suppose vectors are not joined then we need to join them by shifting one vector using parallel shifting. Some examples are shown below:

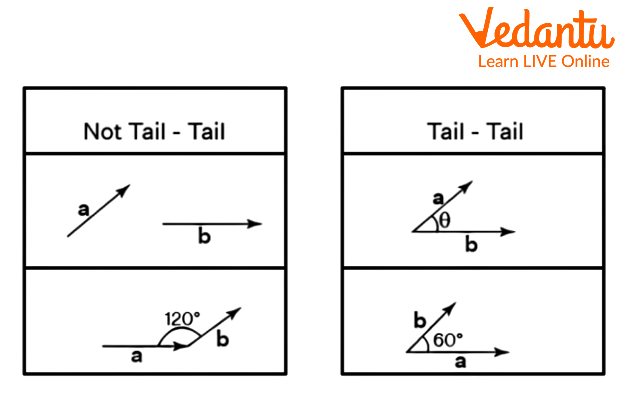
Angle between Two Vectors

Also, the angle between two vectors always lies between\[{{0}^{\circ }}\]and\[{{180}^{\circ }}\]. Next, we can find the angle between two vectors in both 2D and 3D using:

i) Dot Product / Scalar Product

ii) Cross Product

the cross product formula involves the magnitude in the numerator, but the dot product formula doesn’t. 

Position Vectors, Displacement Vectors, and Unit Vectors

• A position vector is a straight line used to find a given point's position with reference to its origin. It starts at the origin and then terminates at any arbitrary point. And as the point moves, the position vector will change in direction or length, or both. 

• For example, the position vector AB means a vector that starts from A and ends from B. Thus, the position vector helps us find a given point's position or location from the origin (or reference point). 

• Next, to find the change or variation in the position vector of a given object, we use the Displacement Vector. 

• And when a vector is used to specify only the direction and has a magnitude equal to 1, it is called Unit Vector. 

• The magnitude of the unit vector is equal to 1, as no magnitude is required for direction.

Interesting Facts

• Formula for the Vector Equation of a Line is \[\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}\]

• Formula for the Vector Equation of a Plane is \[\overrightarrow{r}\cdot \widehat{n}=d\]

• Using Dot Product, the angle between two vectors is \[\theta  = {\cos ^{ - 1}}\left[ {\frac{{\overrightarrow a  \cdot \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}} \right]\]

• Using Cross Product, the angle between two vectors is \[\theta  = {\sin ^{ - 1}}\left[ {\frac{{\overrightarrow a  \times \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}} \right]\]

• The resultant of the product of a zero/null vector with any other vector is always zero. 

• The formula of the angle between each of the two vectors of the unit vectors i, j, and k is \[{{90}^{\circ }}\].

• Formula to find Position Vector \[A({{x}_{1}},{{y}_{1}})\] and \[B({{x}_{2}},{{y}_{2}})\]then \[AB=({{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}})=({{x}_{2}}-{{x}_{1}})i+({{y}_{2}}-{{y}_{1}})j\] and \[BA=({{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}})=({{x}_{1}}-{{x}_{2}})i+({{y}_{1}}-{{y}_{2}})j\]

Important Questions

1. Write the equation of the line passing through the points \[\left( 5,4,1 \right)\]and\[\left( 7,-2,4 \right)\] in Cartesian form.

Solution: The given two points are \[a=({{a}_{1}},{{a}_{2}},{{a}_{3}})=(5,4,1)\]and\[b=({{b}_{1}},{{b}_{2}},{{b}_{3}})=(7,-2,4)\]. The required equation of the line in Cartesian form is as follows:

\[\frac{x-{{a}_{1}}}{{{b}_{1}}-{{a}_{1}}}=\frac{y-{{a}_{2}}}{{{b}_{2}}-{{a}_{2}}}=\frac{z-{{a}_{3}}}{{{b}_{3}}-{{a}_{3}}}\]

\[ \Rightarrow \frac{{x - 5}}{{7 - 5}} = \frac{{y - 4}}{{ - 2 - 4}} = \frac{{z - 1}}{{4 - 1}}\]

\[ \Rightarrow \frac{{x - 5}}{2} = \frac{{y - 4}}{{ - 2 - 4}} = \frac{{z - 1}}{3}\]

Hence, the equation of the line in Cartesian form is \[\frac{x-5}{2}=\frac{y-4}{-2-4}=\frac{z-1}{3}\].

2. What will be the position vector PQ and QP be for the given two points \[P(4,8)\]and \[Q(-2,10)\]?

Solution: For the given points in the xy-coordinate system, \[P({{x}_{1}},{{y}_{1}})=(4,8)\] and \[Q({{x}_{2}},{{y}_{2}})=(-2,10)\]

The formulas to find the position vector of:

\[PQ = ({x_2} - {x_1},{y_2} - {y_1})\]

\[ = ({x_2} - {x_1})i + ({y_2} - {y_1})j\]

\[ = ( - 2 - 4)i + (10 - 8)j\]

\[ =  - i + 2j\]         

Thus, the position vector PQ is equivalent to a vector that starts at the origin and so this vector is directed to a point of 1 unit that is to the left along the x-axis and 2 units upward along the y-axis.

And,

\[QP = ({x_1} - {x_2},{y_1} - {y_2})\]

\[ = ({x_1} - {x_2})i + ({y_1} - {y_2})j\]

\[ = ( - 4 - 2)i + (8 - 10)j\]

\[ =  - 6i - 2j\]

Thus, the position vector QP is equivalent to a vector that starts at the origin and so this vector is directed to a point of 6 units that is to the left along the x-axis and 2 units downward along the y-axis.  

3.  We are given a point \[\left( 2,-1,3 \right)\]and have the direction ratios of its normal as \[\left( 5,2,4 \right)\]. Find the vector equation of a plane passing through the given point.

Solution: The coordinates of the point\[\left( 2,-1,3 \right)\] can be represented as a position vector \[\overrightarrow{a}=2\hat{i}-\hat{j}+3\hat{k}\]. Also the normal having the direction ratios \[\left( 5,2,4 \right)\]can be represented as a vector \[\overrightarrow{N}=5\hat{i}+2\hat{j}+4\hat{k}\].   

Next, the formula of the equation of a line passing through a point and having a normal is \[(\overrightarrow{r}-\overrightarrow{a})\overrightarrow{N}=0\].

\[\Rightarrow \left( \overrightarrow{r}-(2\hat{i}-\hat{j}+3\hat{k}) \right)\cdot \left( 5\hat{i}+2\hat{j}+4\hat{k} \right)=0\]

Thus, this is the required vector equation of the plane.

Conclusion

The article summarises the vector of equations. Along with this, we will learn new words such as zero/null vector, position vector, displacement vector, unit vector, and many more. Also, we will learn the relationship between vector form and Cartesian form. Then we will learn many new formulas and solve problems related to this topic. When the dot product is 0, then the two vectors are perpendicular to each other. 

We use position vectors to determine the position of a particular point with reference to the origin. At last, we will learn different methods of vector equations of a line and plane. Finally, we will see how to find the angle between two vectors and the importance of zero or null vectors.

Practice Questions

1. Is displacement a position vector?

1.  Yes 

2.  No 

2. Find the angle between vectors \[\overrightarrow a \]  and \[\overrightarrow a \] if \[\left| a \right|=1\], \[\left| b \right|=2\]and their dot product is \[a\cdot b=1\].

1. \[{{90}^{\circ }}\]

2. \[{{60}^{\circ }}\]

3. \[{{40}^{\circ }}\]

4. \[{{100}^{\circ }}\]

3. When two children apply equal forces on a toy but in opposite directions. Will the box move in any direction?

1. No

2. Yes

4. What is the sum of a vector \[5i-2j+k\]and a zero vector?

1. \[5i-2j-k\]

2. \[-5i-2j+k\]

3. \[5i-2j+k\]

4. \[-0i-0j+0k\]

Answers:

1) B

2) B

3) A

4) C

List of Related Articles

• Vectors

• Vector Equation

• Cartesian Form

• Components of a Vector

• Types of Vectors

• Angle Between Two Vectors

• Position Vector and Displacement Vector